Base Division
Division is slightly more complicated than multiplication, if you have mastered multiplication you’ll find division quite straightforward because it relies heavily on it. This might seem confusing but after you’ve seen a couple of examples it will sort of click into place I hope.
In all of the texts I’ve seen on base division there seems to be one commonality, a suggestion that you write out the multiplication table in the base that you’re going to be dividing in, and use it through all steps of the division. As I said above, once you’ve seen an example this will make a bit more sense:
Example 1
Let us consider dividing 645 in base 8 by 7 in base 8:
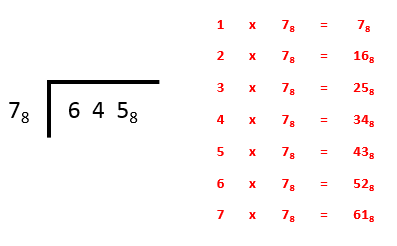
On the left of the picture above you have the expression that we are to be working with, and on the right we have the multiplication table in base 8 (you’ll notice that we stop at ‘7 times’, which is one less than the base and this is the case irrespective of the base you’re using).
Step 1 - ordinarily we would say how many sevens in 6, but even in base 10 we know that that can’t be the case, it would result in a leading 0 which we never do so we automatically go for “how many sevens in 64?”. Now remember that you’re working in base 8 and this is where the multiplication table comes in. Look for the largest value which does not exceed 64, we can see from a table that 7 multiplied by 7 in base 8 comes to 61 in base 8 and this is a value that we enter above the 4 in the answer box.
Step 2 - we subtract 61 from 64 and we place the 3 below the 4, we bring down the 5 and at this point the problem should look like this:
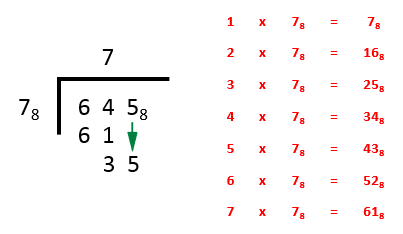
For the sake of simplicity, and ease of reference, I will reproduce the multiplication tables that we are using at each step because if you’re reading this on a computer screen it’s a pest to have to give flicking backwards and forwards
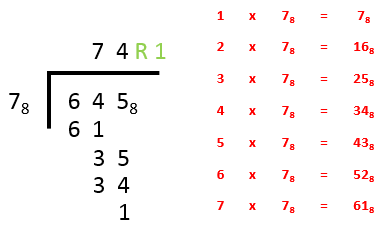
Step 3 - returning to the problem we say “how many sevens in 35?”, Again looking at our table we can see that the highest value which does not exceed 35 is on the 4th line down, “4×78 =348” so we enter a 4 to the right of the number 7 in the answer bar.
Step 4 - we subtract 34 from 35 which leaves one, but this is where the problem ends. We are left with a “remainder of one” and this is how we quote our answer:
Example 2
We will look at another relatively easy example now, when I say “easy” though I am only referring to the fact that we are using bases below 10. When we enter the realm of bases above 10, and start including letters it gets a bit hairy !!.
OK let’s take a look at this example:
“Divide 56328 by 38”
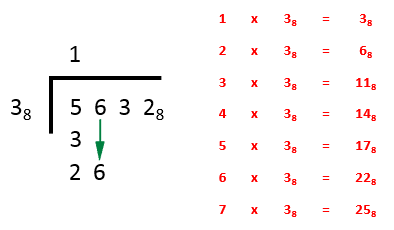
Step 1 - as always, we restate the problem and in these particular cases we will copy out the seven entries of the multiplication tables that we will use in this calculation.

The 3 times table in base 8 has been included so that we can use it to solve the individual steps of the problem. The first question we ask ourselves “how many 3’s go into to 5?” well quite clearly, there is one 3 in 5 with a remainder of 2, so we place a 1 in the answer bar above the 5, subtract the 3 from 5 leaving 2 and drop down the 6 ready for part 2 of the calculation.
Step 2 - we now ask ourselves “how many threes go into 26?” Remembering all the time that we are working in base 8, not base 10 so we refer to our multiplication table once again and we look for results which falls just short of 26 (which really should be described as two six if you are actually speaking it). They answer in this case lies at the bottom of the table, in other words 7 so we enter a 7 to the right of the 1 in the answer bar, subtract 25 from 26 leaving 1 and drop down the 3 ready for the next part:
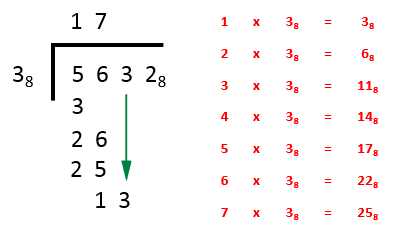
Step 3 - we now ask ourselves “how many 3’s in 13?” And once again we can see from the table that the highest value we can go to is 3 itself. We enter 3 to the right of the 7 in the answer bar, we subtract 11 from 13 leaving 2 and for the final time drop down our remaining value which is also 2:
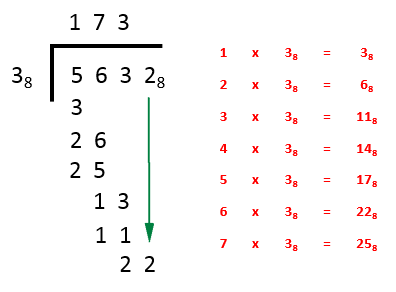
Step 4 – the final part of the question “how many times does 3 go into 22?” can be seen immediately from the table, as 6 with NO remainder value. We place a 6 to the right of the 3 in the answer bar, subtract 22 from 22 leaving 0 and declare the final answer as 17368

So far we have satisfied ourselves in “base division” using bases lower than 10. In these cases we have been confined (rather fortuitously) to the numerals 0 through 9. Things start to become a little trickier and a little bit “stranger looking” when we rise above base 10 because these numbers involve the use of capital letters A, B, C and so on to represent the values 10, 11, 12 and so forth.
Example 3
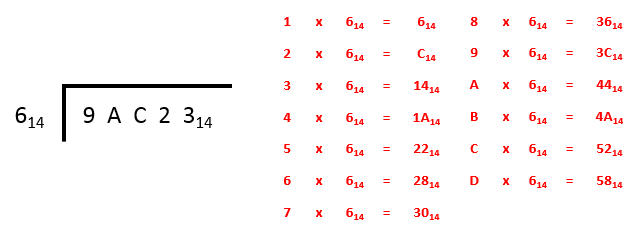
If ever there was an example that would justify writing out the table of multiples, this surely must be it!
As usual, we take our steps slowly and refer to the table (which incidentally as we can see stops at the letter D which has the decimal equivalent of 13, being one less than the base we are using as is always the case).
Step 1 - “how many times to 6 go into 9?” - This is an easy one to start with, the answer of course is 1 with the remainder of 3. We enter a 1 above the 9 (in the answer box on top), we subtract 6 from 9 leaving 3 and we bring down our first value which happens to be A.
Your question should now look like this:
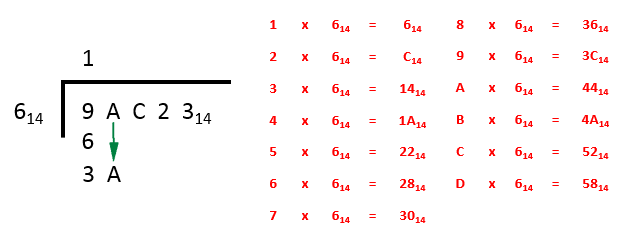
Step 2 - our next question, quite logically is “how many times to 6 going to 3A?”. This is where the value of the table comes in, a little bit of hard work and effort in creating the table will pay dividends when you reach this point in the problem. What we need to do is search for the number of times 6 goes into 3A. If you study the table will you can see that 9×6 will give an answer which is too large, because 3C is bigger than 3A. If we drop back to 8×6 we can see from the table that the answer of 36 suits our purpose. We place an 8 in the answer bar to the right of the 1, we then subtract 36 from 3A which leaves us with 4 and we then drop down the C ready for step 3.
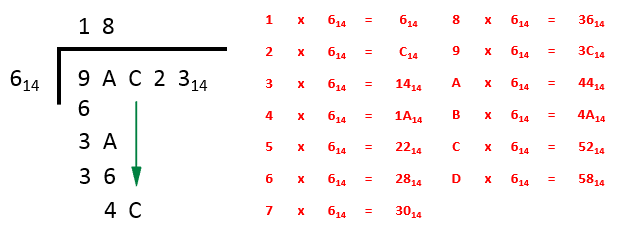
Step 3 - we now have to ask ourselves the question “how many times to 6 go into 4C?” Well, once again we refer to the table and we can see that the answer are looking for is B, in other words 4A since the next available option 52 is too big.
We subtract 4A from 4C, which leaves 2 and we bring down the 2 ready for Step 4.
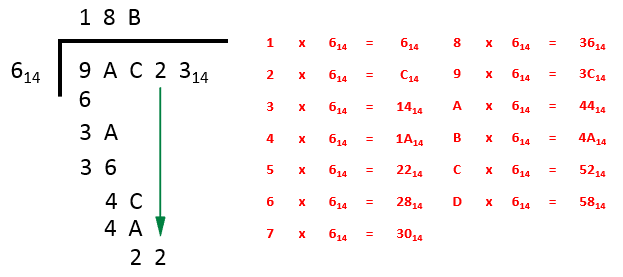
Step 4 - “how many times to 6 go into 22?”, From the table we can see that this is exactly 5 times so we enter a 5 to the right of the B in the answer bar and subtract 22 for 22 leaving 0. We cannot stop at this point simply because we have a 3 left, what we need to do here is bring down the 3 which will sit alone and ask ourselves “how many times to 6 go into 3?”, The answer being 0 so we also append a 0 to the right of the B and this completes the question. REMEMBER that because we couldn’t complete the final division, that 6 does not going to 3 we must regard the 3 as a remainder!
The picture below shows the completed calculation in its entirety.
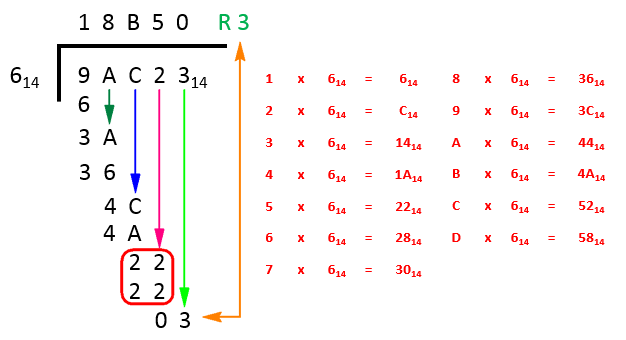
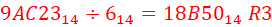
Study the diagram for a moment and you can see all the drop downs that took place throughout the calculation, the reason that there is a remainder can be seen by virtue of the fact that the step before it resulted in an exact value (as shown by the 2 x 22’s circled in red). At this point we have essentially reach the end of the calculation.
Example 4
Example 4 remains in the bases above 10, and introduces a trickier divisor because this time using a 2 digit / 2 character “number” (divisor).
Let us take a look at the question:

As you can see, once again I’ve written out the “base 13” table for the first 12 necessary computations (12 obviously because like before it has to be one less than the base).
We approach this problem in absolutely no different way whatsoever to the previous one, starting at step 1 when we ask ourselves the following question:
Step 1 - “how many 6A goes into A?”, Well clearly it can’t and because we don’t use leading zeros we just simply say okay let’s change this to AB, and we ask ourselves the question “how many 6A goes into AB?”.
Refer to the table, if you need to, then convert some of the numbers back to base 10 but you will see that AB is larger than 6A but smaller than 107 (6A base 13 is 88 base 10 and AB base 13 is 141 base 10, however 107 base 13 is 176 base 10 which as you know is more than 141, so we need to select the answer where 141 in base 10 gave the appropriate base 13 response, in other words 6A).
Study the paragraph above, study it well because it is quite confusing. The outcome of this is that we enter 1 into the answer bar above the B in “AB”.
We subtract 6A from AB which leaves 41, we bring down the C to make the next subject 41C and we ask ourselves the question:
Step 2 - “how many times does 6A go into 41C?”
Our problem now looks like this:
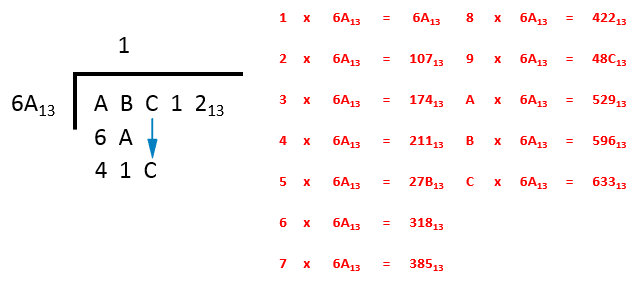
Considering the question we are asking ourselves in step 2, we look at the table once again to find an appropriate number. If you take a look at “7 times” you can see that the answer is 385, if we go one further up to “8 times” we exceed 41C (we reach 422) so we can see that “7” is the appropriate result which would place on the answer bar to the right of the 1.
We can see that 7 times 6A is 395 which we subtract from 41C leaving 67, we drop down the 1 to make 671, the problem now looks like this:
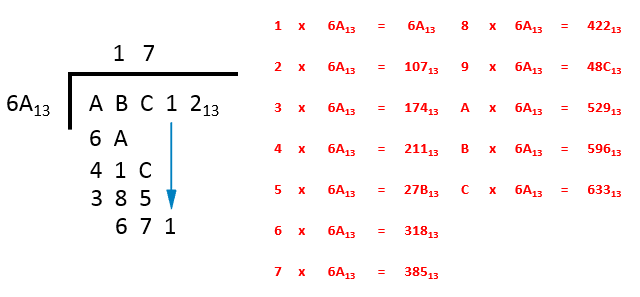
Step 3 - “how many times does 6A go into 671?” - If we look at the table we can go directly to the end, “C” fits the bill quite nicely at 633 base 13. We put C to the right of the 7 in the answer bar and we subtract 633 from 671 leaving 3B. We drop down the 2 making 3B2 and prepare for the final step.
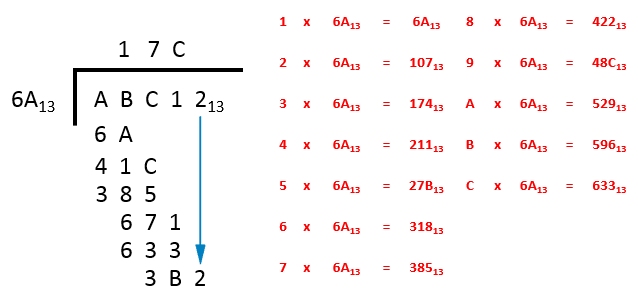
Step 4 - “how many times does 6A go into 3B2?” - Look at the table and you can see that the answer is 7, had we have chosen 8 we would have exceeded the value allowed (422 as in one of the previous steps). We place a 7 in the answer bar to the right of the C, we subtract 385 from 3B2 which leaves 2A.
In fact, this is where the calculation ends because 2A is in fact the remainder. The completed question is shown in the next picture.
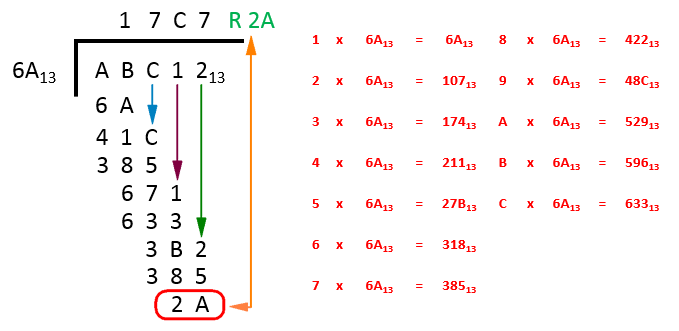
This does seem rather confusing I agree, some texts on the Internet suggest that the best way to do these complicated calculations is to convert the divisor and the dividend to base 10, perform the division and then convert the result back to the desired base.
I’ll run through this quickly:
ABC12 in base 13 is 311,820 in base 10 and 6A in base 13 is 88 in base 10. If we perform the division in base 10, here is our answer:
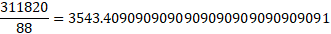
That is, 3543 with a recurring decimal part of 0.4090909 and so on. Take a look at the 3543 part which is a base 10 number and convert it to base 13, your answer will be 17C7:

Well, that explains the first part, but what about the decimal bit?. Well, that part is in fact a number of “88ths” from the division, and to find out how many we multiply the decimal by 88 which gives a value of:

And what is 36 base 10 in base 13? - 2A !!
