Manipulation (Transposition) of Algebraic Expressions
As we have seen before in algebra, an equation is an expression split by an equality such that one side equals the other.
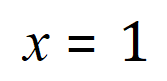
The above expression is perhaps as simple as it gets, clearly “x” does indeed “equal one” for the expression to qualify as an equation.
But what happens when we have more complicated expressions, and we need to find the value of “x”?
Generally, there are several ways to solve these issues:
- Collecting ‘like terms’
- Factorisation
- Graphing
Collection of ‘like terms’ is the easiest for simpler expressions:
Example
Q. Solve for ‘x’:
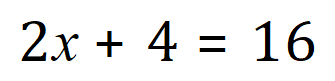

This isn’t so bad, because the ‘like terms’ are already ‘collected’ on the left side of the equation, so what we need to do now is a little bit of ‘left side’ versus ‘right side’ manipulation:
Subtract 4 from both sides:
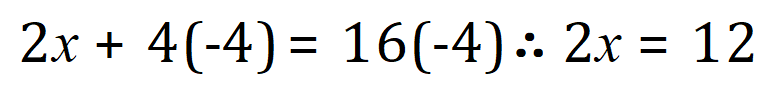
Divide both sides by 2
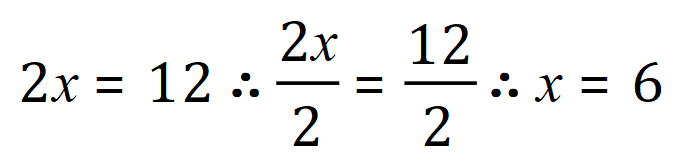
And here we have our solution.
Now things are going to get a bit tougher….look at this one:
Solve for ‘x’


Not as easy this time as there is a bit more tidying up to do but as you get better you will be able to use the ‘bring it across and change the sign’ method when collecting ‘like terms’
Bring 8x across and change its sign:

Take +6 across and change its sign:

Tidy up: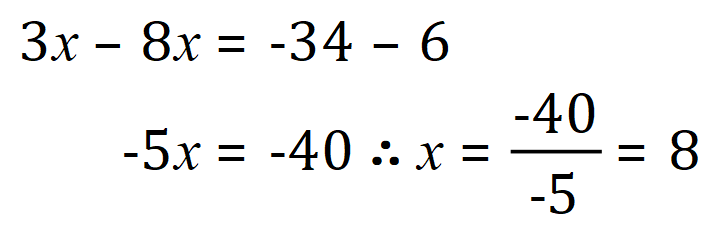
This takes some getting used to, and the benefits of checking back with your new found value for ‘x’ can’t be stated strongly enough.
Now the questions in the exam might not be simply stated "do this then that etc", like with the simultaneous equations we have seen before, you might need to work through a short scenario to establish the question for yourself or you might be given something that looks just that little bit different:
Q. In the diagram shown, the perimeter of the triangle and the perimeter of the rectangle are equal. Use this information to obtain an expression for 'x' in terms of 'y'.
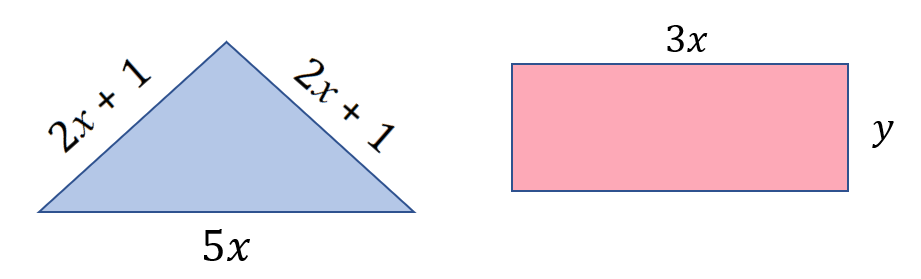
A. This isn't quite as horrifying as it might appear. Write out expressions for the perimeters of both shapes and make these expressions into an equality (as you are told they are equal).

The upper expression shows the algebraic representation of the perimeter of the triangle and the lower expression is the algebraic representation of the perimeter of the rectangle, we now show this as an equality:
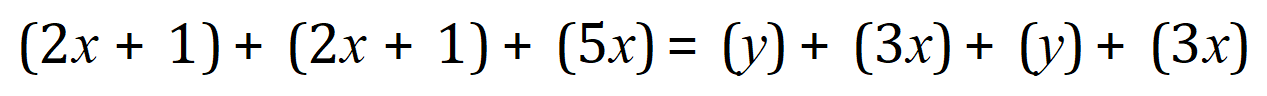
Let's do some housekeeping on this equation. In this particular case the parentheses aren't really necessary, I have just used them to show how elements can be grouped, however if there were any 'minus' signs about you would need to take care when removing the parentheses.
Removing parentheses:
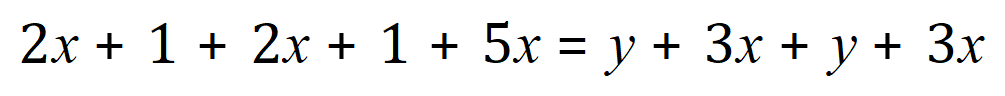
Collecting like terms:

This looks a bit more familiar now.
Subtract 6x from both sides:

Subtract 2 from both sides then divide both sides by 3:

Let’s have a go at a tougher one now……
Q. Rearrange the expression below to make ‘a’ the subject:
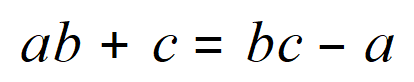
Arguably this is about as nasty as a GCSE examiner would make it, but who knows??
Step 1 – restate the problem

Step 2 – Collect the ‘a’ terms on the left (add ‘a’ to both sides…remember?)
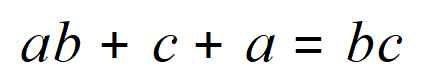
Step 3 – Collect the ‘c’ terms on the right (subtract ‘c’ from both sides)
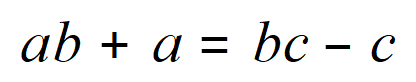
Step 4 – Now it gets naughty, you have to bring in some factorisation to release the ‘multiplied a’ and ‘b’ terms….see if you follow this (by expanding back out)
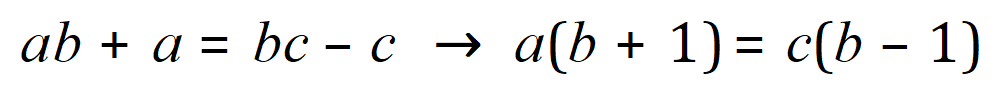
Step 5 – Got that?.....OK divide both sides by (b+1)

You can easily cross check by letting a=1, b=2 and c=3 and you will indeed see that:

In different parts of this book you will see that I regularly use the expression "restate the problem" and you might think that this is an unnecessary step which just takes up time. Arguably you are correct, but the reason that I suggest this is that when someone is marking your work (it could be your teacher or the actual examiner) it is useful for them to be able to see all of the steps you took. So if you have accidentally written the question down incorrectly (for example you have written a minus somewhere instead of a plus or vice versa) then the chances are that you will not arrive at an answer that looks in any way sensible (exam questions are often crafted to give "obvious" looking answers) or you will produce a long artistic answer to the wrong question. If the examiner can see where you started from you may get credit for working.
>> Questions <<