Simultaneous Equations
Previously, in other chapters of the book with regard to algebra we have seen how to solve equations for unknown variables, for example the type of simple equation that appears elsewhere in this book:
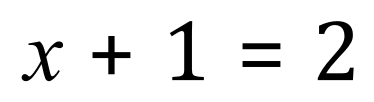
Tells us that there is a value for ‘x‘ which satisfies the equality. At this point, by inspection you can tell me that ‘x’ equals one. However, consider the following equation, not unlike the first one but clearly not as easy to solve in fact not easy to solve at all:

You might be forgiven for thinking, “well this isn’t difficult, because ‘x’ equals 1 and so does ‘y’” and you would be correct… on this occasion!
What if we said ‘x’ was 3?, indeed if we then said ‘y’ equals minus one then the equality would be satisfied once again. Let’s carry on with this argument, what about if ‘x’ was -12 and ‘y’ was +14 then once again the equality stands true. You should now be realising that you cannot give a hard and fast value for 2 variables in the same equation because there is an infinite range of values for ‘x’ which can be added to a corresponding value for ‘y’ to satisfy this equation.
As it stands, we have an infinite number of values of 'x' and 'y' which would solve this equation.
The way that we solve these equations is to take second equation involving the same variables, almost always with different values and therefore a different value for the equality on the right-hand side, we then manipulate the equations arithmetically to arrive at a value for one of the variables, it usually doesn’t matter which one and then to use that value in one of the two original equations to arrive at the value for the second variable.
Because we process the equations together, or simultaneously, you won’t be surprised to find that they are called “simultaneous equations” :-)
There are 4 main methods for solving simultaneous equations, the first, and probably by far the simplest and most popular is the method I’m going to look at first, “Solution by Elimination” and the second which is probably a little bit harder to get your head round is "Solution by Substitution. Graphing the equations and looking for common values of 'x' and 'y' where the lines cross is a good third method but by far the most demanding is the fourth method “Solution Using Matrices” which is not easy, but is very elegant in its approach.