Using Elimination
As I explained in the opening gambit to this particular chapter, there is no single solution to the sort of equation you see below. There are an infinite number of values of 'x' and 'y' which will satisfy the equality of 3 but if we ‘pair’ it with a second equation and solve them simultaneously we can arrive at values for ‘x’ and ‘y’.
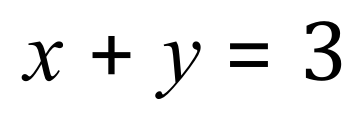
Example 1:
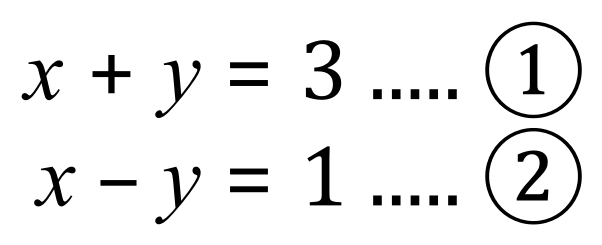
You will find that simultaneous equations are usually numbered like this, because when we start adding and subtracting, or otherwise manipulating the variables it can become laborious to have to keep writing out the equation, so we usually just refer to the number of the equation and the operation of performing on it. You will see examples of this in a short while.
The object of simultaneous equations is to manipulate them so that one of the variables disappears, this will only receive an expression involving one variable and an equality from which we can deduce the value of the variable and, as I mentioned above, then use that variables value to arrive at the value of the second one.
If you look at the equations above, equation (1) and equation (2) you should be able to see that if we add them together, ‘y’ will disappear because +y and -y added together become 0.
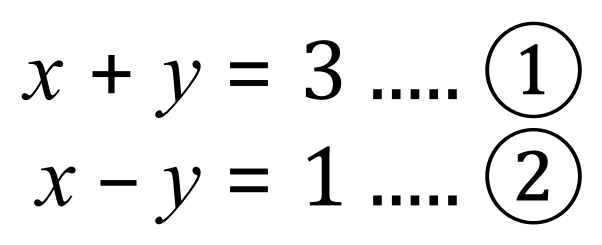
Adding equations (1) + (2) together, remembering the rules for the addition of positive and negative numbers:
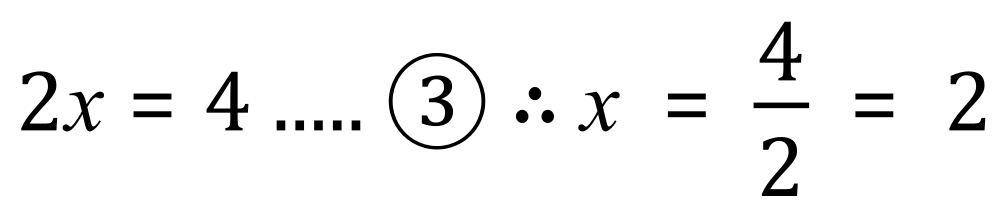
Let’s just study this for a bit, I’ve restated the equations, numbering them 1 and 2, I have then indicated on the left-hand side that I intend to add the equations together and the result of that addition I’ve called equation 3. On the same line, just for convenience, I have simplified equation 3 to arrive at a value for ‘x’.
Now that we know that ‘x’ equals 2 we can “substitute” this value into either equation 1 or equation 2 to calculate a value for the remaining variable ‘y’. Usually we choose the simpler of the 2 equations (for obvious reasons) but in this particular case as they are both simple we don’t need to worry about this.
For argument sake though, let’s choose equation 2:
‘Substituting for ‘x’ in (2)’

Study the last 2 lines for a moment, we are replacing the variable ‘x’ in equation 2 with its value, and it is usual to actually state what we are doing so that any person reading your work understands your logic, also this will help any examiner to decide how many marks to give you should you ultimately arrive at the wrong answer (remember even if you get the question wrong your teacher/examiner will probably still give you some marks for your working, provided they can understand what you are doing). We now know that x equals 2 and y = 1, we have therefore solved our first pair of simultaneous equations!
Example 2
Let’s take another look, this time we will work on an equation pair which is a little bit more complicated than the first one:
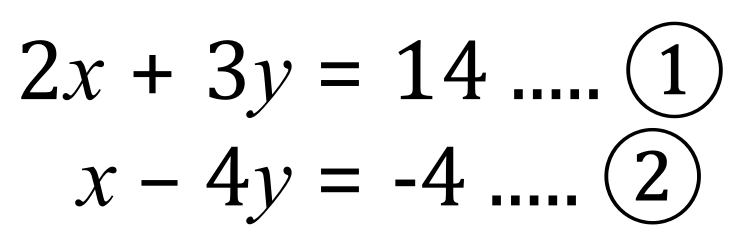
Yes, I’m afraid to say it, but nasty negative numbers crawl in anywhere so in some cases like this you have to be really careful when you are adding and subtracting when it involves negative numbers. We have numbered our equations 1 and 2 so we are ready to go.
Step 1 - we need to make a decision which variable to eliminate first, if you take a look at the equations you can see that if we double equation 2 and then subtract the newly formed equation 3 from equation 1 we will get rid of the ‘x’:
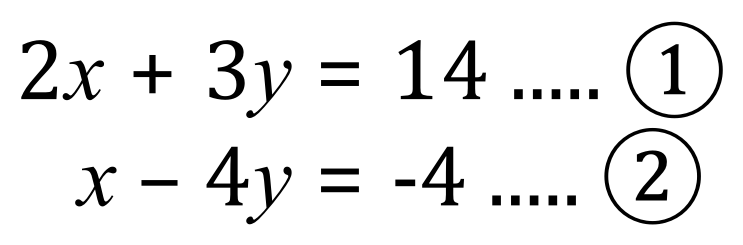
(2) x 2:
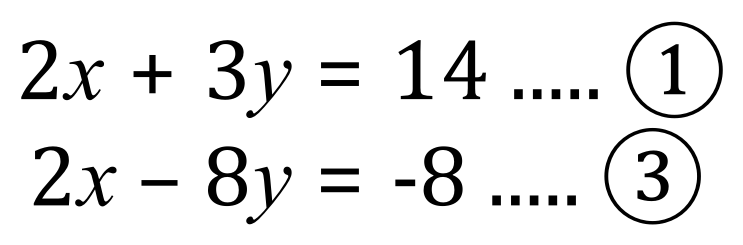
(1) – (3):
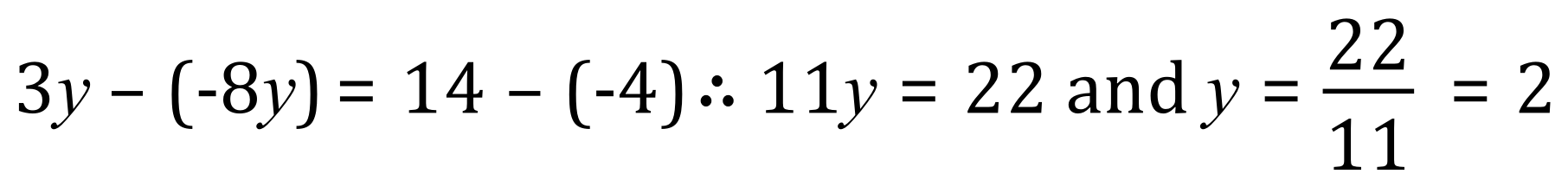
As I said before, when we come to make the subtractions be aware of subtracting negative numbers.
Now that we have obtained a value for ‘y’ it is fairly straightforward to see that equation 1 (because it doesn’t involve any negative numbers) is probably the best equation to substitute our newly found value for ‘y’, to obtain a value for ‘x’:
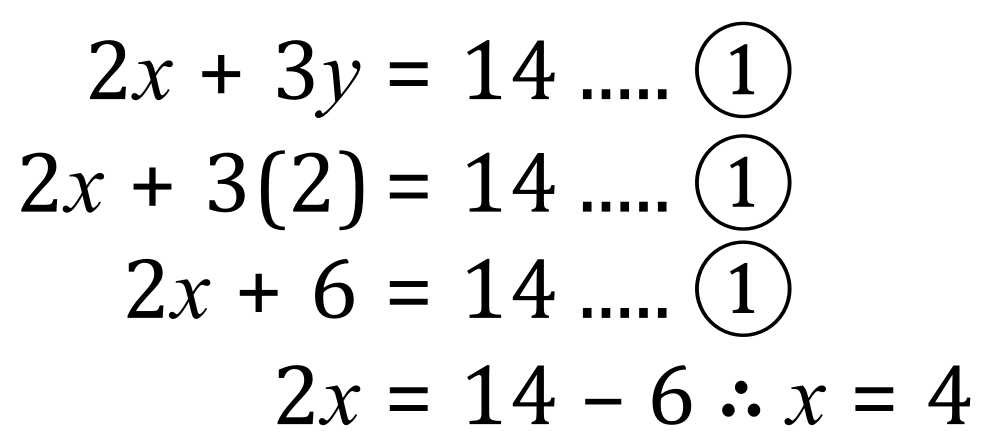
We have now solved our simultaneous equations, ‘x’ equals 4, ‘y’ equals 2.
It could be that you are just given a pair of simultaneous equations and asked to solve them for ‘x’ and ‘y’ respectively or you may be given a scenario, from which you will be expected to construct the equations yourself and then go on to solve them.
Scenario Based Example 1
Q. Last week I took two my friends to the local carvery. We each enjoyed a carvery meal and one of my friends drank a Diet Coke to go along with it as did I. This week my friend who dislikes Diet Coke came with me to the same carvery but our other friend could not make it so we both enjoyed a carvery but only I had a Diet Coke with mine.
Last week’s bill came to £22, this week’s bill came to £14.
How much does a carvery cost and how much does a Diet Coke cost at our local establishment?
Step 1 - First of all, examine the question and let us call a carvery ‘x’ and a Diet Coke ‘y’. Reading the question, the first week we had 3 carveries between us and 2 Diet Cokes and the bill came to £22. The second week we shared 2 carveries and because my friend doesn’t like Diet Coke, only I had one.
From this information we can construct 2 equations:
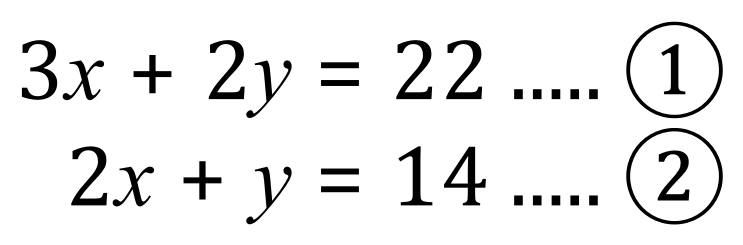
Step 2 - we need to make a decision which variable to get rid of first, if we consider equation (2) and double it we can perform subtraction:
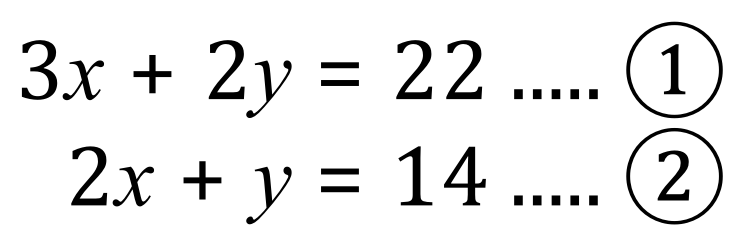
(2) x 2:

(3) – (1):
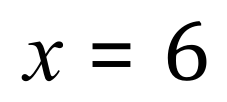
Remember to always indicate along the left-hand side what you are doing with the equations, the first step shows that I’m multiplying equation by 2 and the second step shows that I’m subtracting equation 1 from equation 3, which leaves a very simple expression giving an immediate value for ‘x’.
Equation 2 seems to be the ideal candidate to substitute our newly found value for ‘x’:
“Substituting for ‘x’ in (2)”:
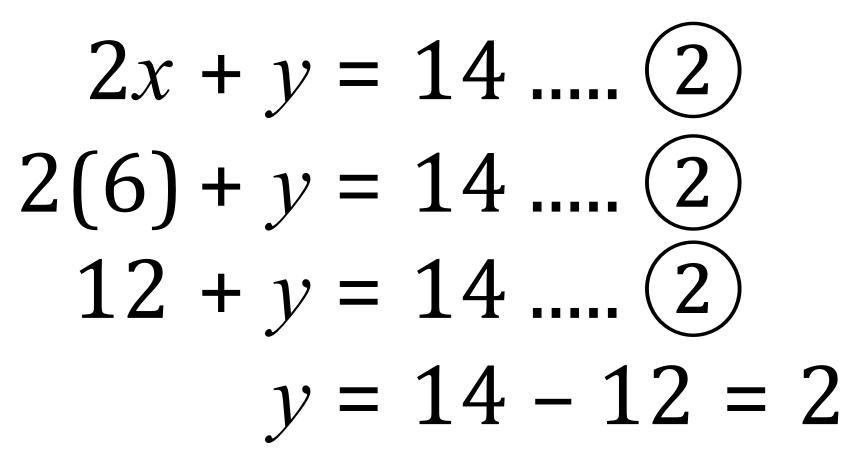
We have now finished our question, ‘x’ = 6 and ‘y’ = 2, that is:
The price of a carvery is £6 and the price of a Diet Coke is £2.
Scenario Based Example 2
Q. I had to work over the weekend, but my boss told me that any money I spent on food, the company would reimburse me provided I kept the receipts or could tell him how much the food cost.
On Saturday I went to McDonald's, I was feeling quite hungry so I bought 3 Big Macs and a McCFlurry. This came to £11. On Sunday, I felt quite greedy and decided to have 2 Big Macs and 3 McFlurries, this time the bill came to £12.
Unfortunately I lost my receipts but the boss said he would pay me provided I could show him how much each item cost, that is how much was a Big Mac and how much was a McFlurry?
Usually the questions aren't quite this wordy because you might be doing this under exam conditions in a test, it would probably be fairer to give you this sort of question for homework. Anyway, let's start looking at how to solve it:
As is the case with most simultaneous equations, in fact probably all of them, we have to decide what we are going to call 'x' and what we are going to call 'y'. Let's take a look at what we did on Saturday first of all, let us call a Big Mac 'x' and a McFlurry 'y'

You should be able to see that because I had 3 Big Macs and 1 McFlurry coming to a total of £11, equation 1 is correctly representing this.
Let's do the same for Sunday:

Okay, you should now be able to see that I have correctly represented what I bought on Sunday in equation form. We now have a pair of Simultaneous Equations and we need to decide which one out of 'x' or "y' we're going to eliminate first (as we are going to use elimination method, this is likely to be the method that you would be expected to use anyway).
It doesn't really matter which variable you eliminate first, but just for the sake of simplicity I believe that 'y' will be the simplest option if we multiply equation 1 x 3:
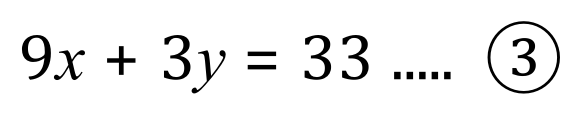
Pause for a moment if you can't see where this came from. When you're ready to continue, carry on reading.
Now if we subtract equation 2 from the newly created equation 3, we can eliminate 'y' and solve what is left for 'x'
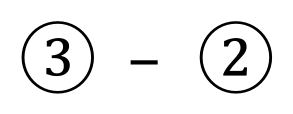
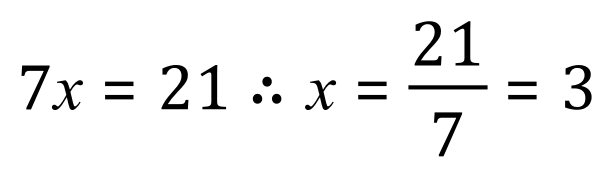
We have now established that a Big Mac costs £3. Equation number one is the simplest overall "original" equation and so we substitute our newly found value for 'x' to obtain a value for 'y' :
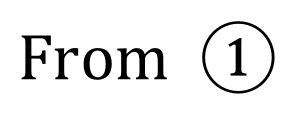

We have now established that a McFlurry costs £2. Armed with this information, not only have you solved your simultaneous equations but you should hopefully get all your money back :-)
It is always advisable to finish off the answer to the question with a statement of what you found, it is tidy and it rounds off the answer, making the teacher/examiner’s life easy (always a good thing!).
The Rules Of Elimination:

To summarise and conclude this section, I have developed a set of "rules" which are quite useful to follow when solving simultaneous equations by the elimination method. I will now state these rules, punctuated by a working example of how I would apply them:
- Make sure that the first thing you do is number the equations (1) and (2) because this makes it easier for anyone looking at your work to examine the steps you've taken. If a teacher/examiner can follow your thought processes you are likely to receive marks for working even if you end up with the wrong answers.
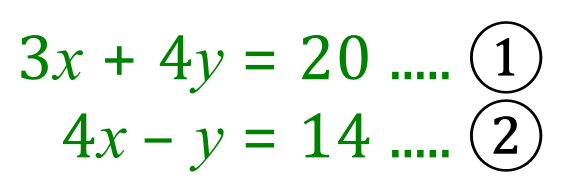
- Look at the variables 'x' and 'y' or whatever letters they have been assigned, and try to identify which variable you are going to get rid of first. As the "elimination" label suggests, you will "eliminate" one variable, work out a value for the remaining one and then "back substitute" into one of your original equations to obtain a value for the remaining variable.
Remember that in this case you will be using addition or subtraction to combine the equations, so you need to look at a way in which one of the variables can be eliminated during the addition or subtraction of your equations.
I have identified "y" as the variable I will eliminate as I can remove it by simple addition if I make the "-y" into "-4y".... see rule 3. - Use multiplication if necessary to make one of your variables easy to eliminate, for example if you have "+4y" and "-y" in equations (1) and (2) respectively you would consider multiplying equation (2) by 4 which would mean that the variable 'y' could be eliminated by simply adding 2 equations together ("+4y"+"-4y" = 0).

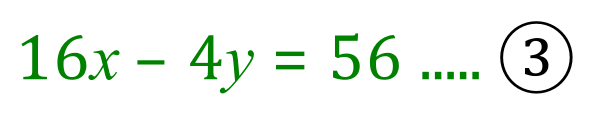
- Perform the addition or subtraction to eliminate your chosen variable, and solve the remaining equation for the value of the remaining variable.
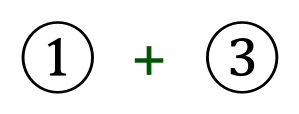
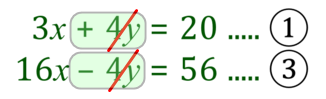
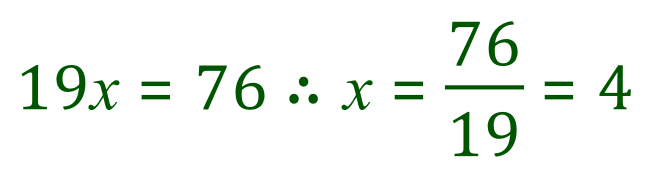
- Select one of the two original equations (the simplest one out of the two is usually the best option) and substitute your newly found variable value into it, to establish a value for the remaining variable.
From (2)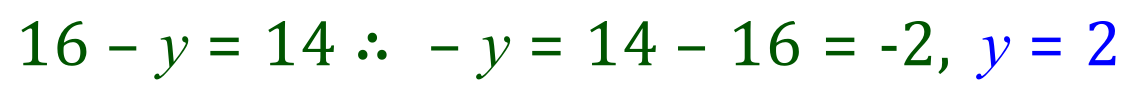
- If time permits, if this question is being attempted in an examination or time to test, choose one of the equations and substitute both values for your newly found variables to make sure that they are indeed correct. If this is a homework question, you should do this anyway.
- State on a new line at the bottom of your result the values for your variables.
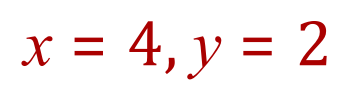
>> Questions <<