Using Substitution
Simultaneous equations do not only have to carry 'x' terms, they can also carry quadratic 'x2' terms which can make the solving of a pair of such equations slightly more complicated, as this will lead to two values of 'x' and two values of 'y' satisfying the pair of equations.
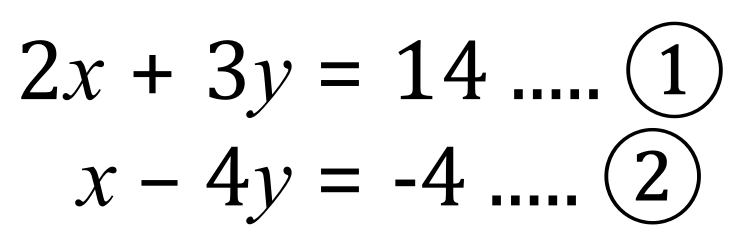
The 2 equations above were used in the previous section, and from that we already know that the values of 'x' and 'y' are 4 and 2 respectively. What I intend to do now, is used the "substitution" method to show this again.
First of all, let us rearrange equation 2 so that it is in "terms of x" :
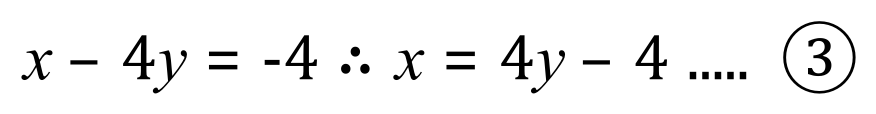
We now take our new expression for 'x' from the rearranged equation (2) and substitute into equation (1)
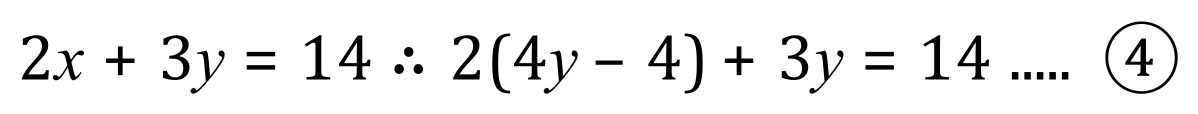
After a little bit of tidying up of equation (4) :
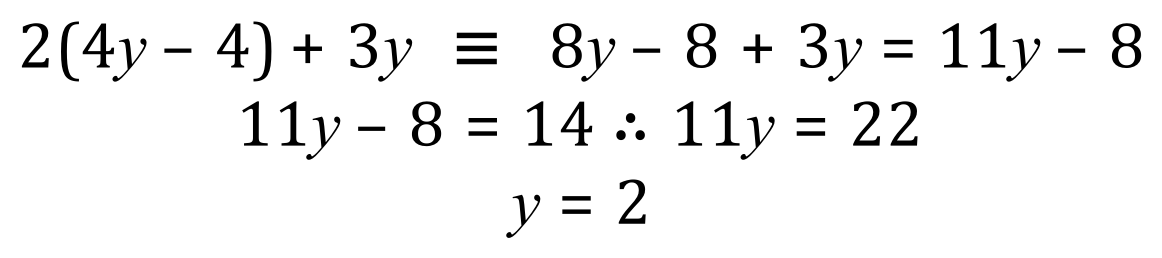
We can now take our new found value for 'y' and substitute into any of the equations. Equation number (2) seems to be the most obvious as it is the simplest:
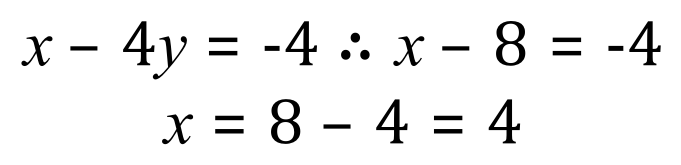
Lets take a look at another, just to make sure we have got it, then we will look at a set of Simultaneous Equations where there is a quadratic, or x2 term.
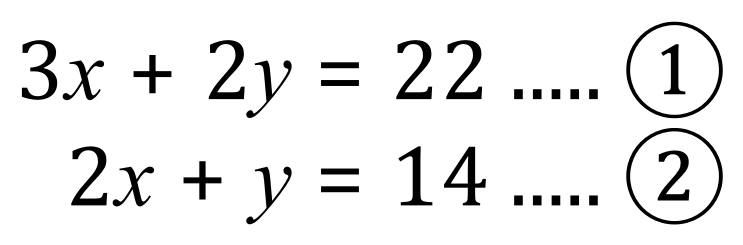
From (2):
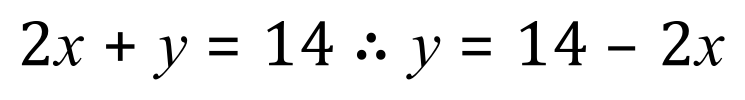
Substituting into (1):
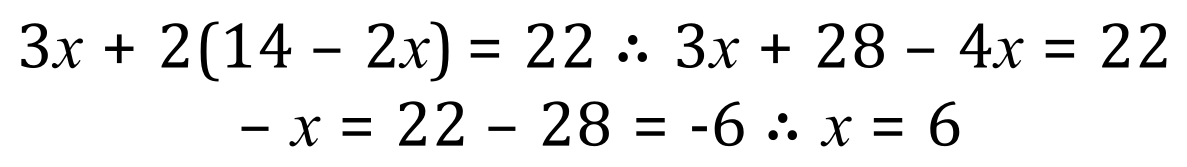
From (2):
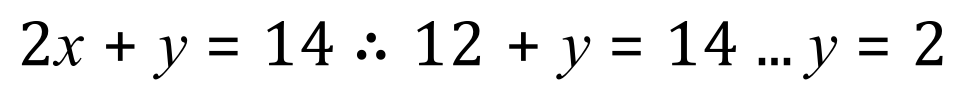
A simple back substitution will show that the values 'x' = 6 and 'y' = 2 are correct.
Let's now take a look at the situation where we have a quadratic function, under these circumstances a pair of simultaneous equations will have 2 sets of solutions. The substitution method for solving simultaneous equations requires that we establish the values of both sets of solutions.
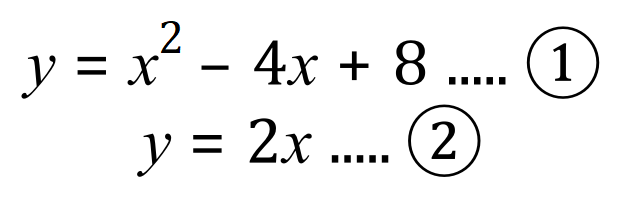
It is fair to say that the first time I came across this sort of set of simultaneous equations I was quite bemused, however if you approach them logically you will see that commonsense steps in and the equations are not quite as confusing or scary as they might first appear.
To solve this particular set, we simply substitute the value for 'y' in equation (2) into equation (1):
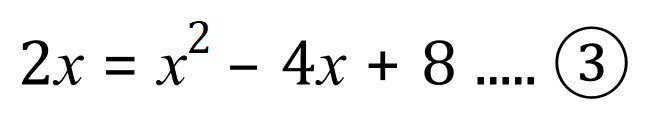
We now rearrange equation (3) to form a standard quadratic equation which equates to 0, then we solve it in the usual way for quadratic equations to obtain 2 values for 'x':
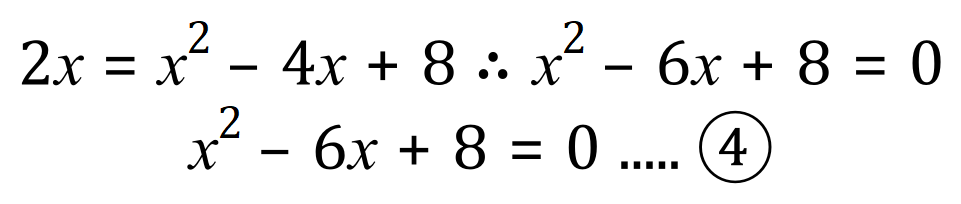
By whichever method you prefer, solve equation (4) to obtain 2 values for 'x' which satisfies, in other words find the roots of the equation. I prefer the inspection method where we look at it and say to ourselves "we need to numbers which, added together come to -6, but which when multiplied together come to +8" it shouldn't take long to see that -2 and -4 fit quite nicely.
We can therefore state that the values for 'x' which solve the quadratic equation (4) are 'x' = 2 and 'x' = 4.
Now that we've established the values for 'x' , being the roots of the quadratic equation, we can now use these individually in one of the original equations to establish corresponding values for 'y'. The simplest equation of course is equation number (2) from which it should be fairly straightforward to see that if 'x' = 2, then 'y' = 4 and if 'x' = 4 then 'y' = 8.
It is a good idea to conclude your question with a statement of the answers you have obtained:
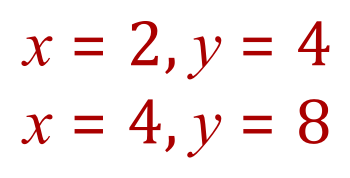
>> Questions <<