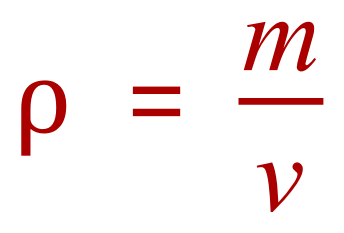Density and States of Matter
Density is a subject which is covered in chemistry physics and mathematics. For the purposes of this section will just look at the formula for density and the way in which we can measure the densities of regular and irregular shaped objects.
Let us take for example, a simple cube.
|
|
There are two things we need to know about this cube before we can calculate its density. If we take a look at the expression for density we will be able to see what these two things are: |
|
|
Where the Greek letter "ρ" (rho) represents density, "m" represents mass and "v" represents volume.
Q. Calculate the density of a cube which has a side length of 3 cm and a mass of 27 g. State your answer in kilograms per cubic metre.
A. We are told to state the answer in kilograms per cubic metre so the first thing we should be looking for is whether or not the values we have been given are in those units, if they are not we should change them now. 3 cm is 0.03 m and 27 g is 0.027 kg.
Now that we have our mass and volume in the appropriate units we can calculate the density.
Using the expression as given above and substituting our known values:
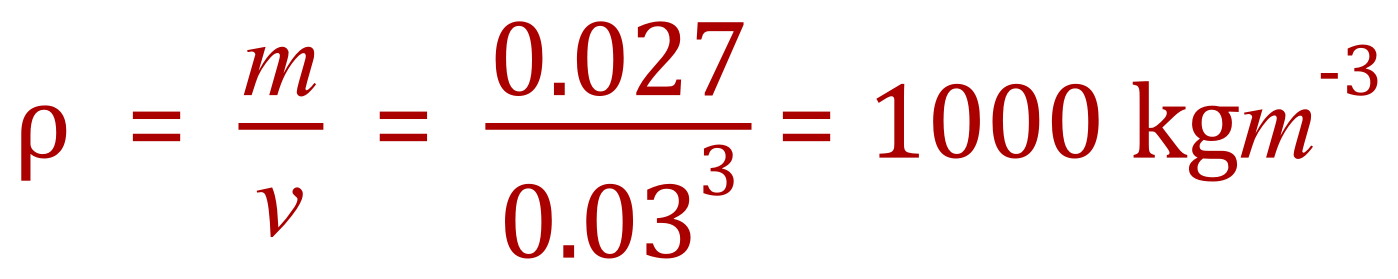
Q. Calculate the density of a steel cube, with a side 10 mm and a mass of 94 g.
A. Once again, because the units of density are kilograms per cubic metre we need to make sure that our given values are in the correct units. We can see that in neither case they are so we convert them first.
10 mm is 0.01 m and 94 g is 0.094 kg. Using the same formula as before, we can now calculate the density.
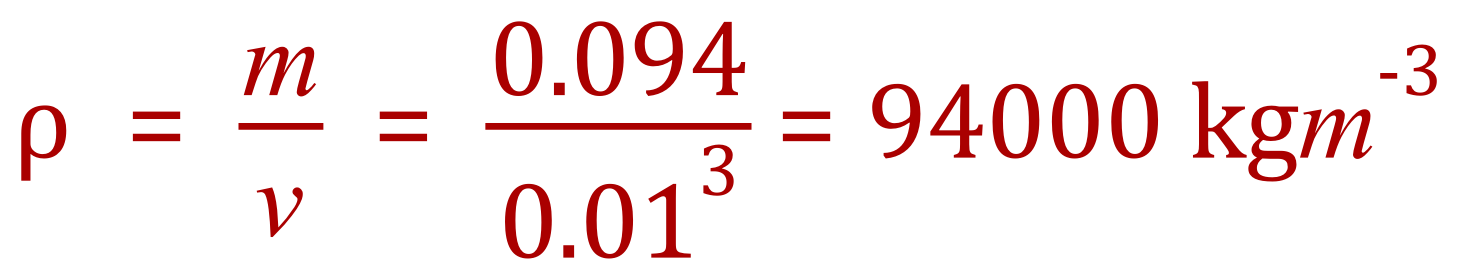
Of course, we don't always have the luxury of calculating the density of cubes! If we are given a different (but regular, see later) shape such as a cylinder, a sphere or a triangular prism we need to know the formula to calculate the volume of these items before we can calculate the density.
>> Useful Mathematical Formulae <<