Irregularly Shaped Objects
If we have a regular object we can usually simply measure the dimensions and then apply a simple formula to calculate the volume. A scale, or balance will give us the ability to measure the mass of the object and therefore the density is quite easily calculated. But what if the object is irregular?
For example we wish to measure the density of a stone, but of course stones come in all shapes and sizes, so to try to do it arithmetically would be near enough impossible. Fortunately there is a fairly straightforward way to do this sort of thing in the laboratory, and we owe it all to the Greek philosopher Archimedes.
Click to read the story >> Archimedes Principle <<
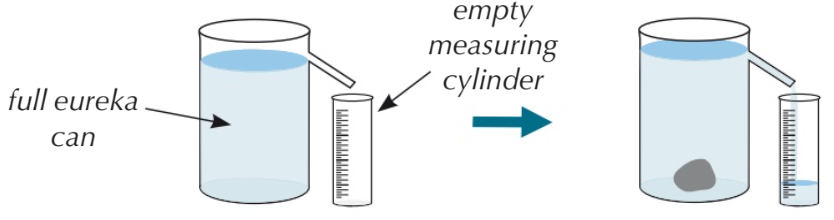
Archimedes discovered that a body, fully immersed in a liquid will displace its own volume. The "Eureka can" is set up in place, usually on a tripod and filled to a point just above the opening of the spout. The excess water is allowed to run away until the level of water is at the same height as the bottom of the opening.
The object whose volume is to be measured is very carefully lowered into the can until it is completely submerged (note that the object must be completely submerged otherwise you will not measure its complete volume). The displaced water is captured in a measuring cylinder and the volume of water measured will equal the volume of the stone displacing it.
Q. A stone with a mass of 245 g is lowered into a Eureka can and the displaced water is collected in a measuring cylinder. 10.6 mL of water is collected in the measuring cylinder. Calculate the density of the stone, in kilograms per cubic metre.
A. Because the question is asking for the answer to be specified in certain units, it would be advantageous to convert our given values to those units before you calculate anything.
245 g is 0.245 Kg
10.6 mL is 0.0000106 m3
The calculation of volume takes into account that water has a volume of 1 cm³ per millilitre.
The formula for density is:
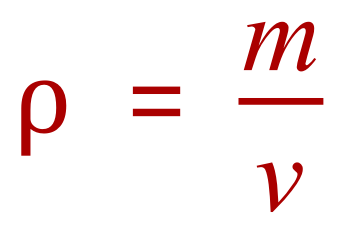
Substituting our values of mass and volume, we arrive at the following density:

You must remember though that 23,113.2 is only part of the answer. You need to quote your units. In this particular case this is quite easy, but you can also perform a mathematical operation on the units to make sure you represent them properly:
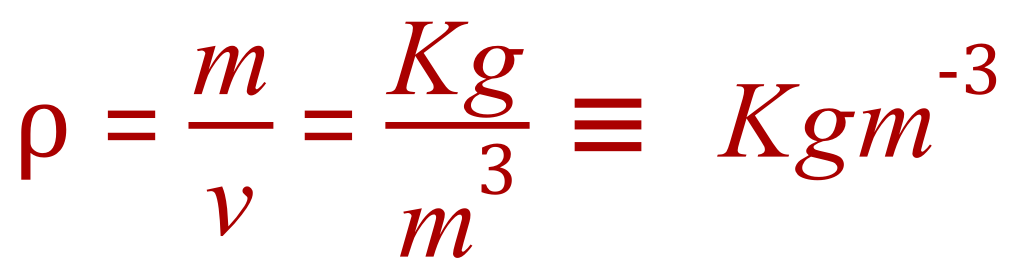
This is pretty heavy stone, at 23 tonnes per cubic metre.
At GCSE level, units are usually quoted with "/" between them, so for example this would be shown as Kg/m3 and not as it has been shown in the equation above. The "negative exponent" format (if you like) is something you're likely to encounter at advanced level and beyond.