Division of Matrices (?) - The Inverse Matrix
Eventually this section will have covered most of the main arithmetic operations that can be performed on matrices, in many cases displaying similarities to the arithmetic of simple integers. We can multiply matrices together in just the same way that we can multiply numbers together but as we have already seen the commutative rule of arithmetic does not always hold.
There is no easy way to divide matrices, but in certain circumstances the equivalent operation of a division can be conducted in much the same way that we can "divide using multiplication" in arithmetic.
Let us take a look at an example:
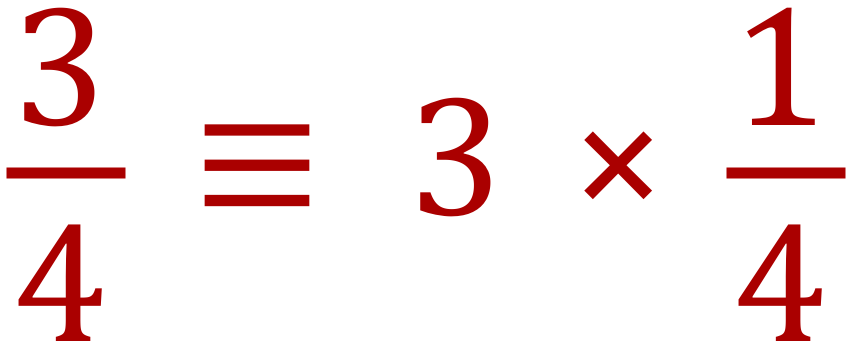
We can see that division can be accomplished by multiplying one of the numbers by the reciprocal or inverse of the other. 3 multiplied by the inverse of 4 gives the same result as 3÷4. We can do the same thing with matrices (with some limitations, this must be noted).
If we consider a matrix A, we usually denote the inverse of the matrix as A-1
To calculate the inverse of a matrix we use the following formula (note that this discussion will stick to simpler 2×2 matrices, there are ways to calculate the inverse of higher level matrices but this involves mathematics which is way beyond the scope and intention of this section).
|
|
then |
|
The first part is simply a fraction, determined by the difference between element products "ad" and "bc". If this evaluates to 0, there cannot be an inverse to the matrix because this would require division by zero which of course is not allowed.
The computation "ad-bc" is known as the "determinant" and is usually written as "det A". A nonzero determinant tells us that the matrix is invertible, a zero determinant tells us that the matrix is non invertible.
Example: given the matrix A, if possible produce the inverse matrix A-1
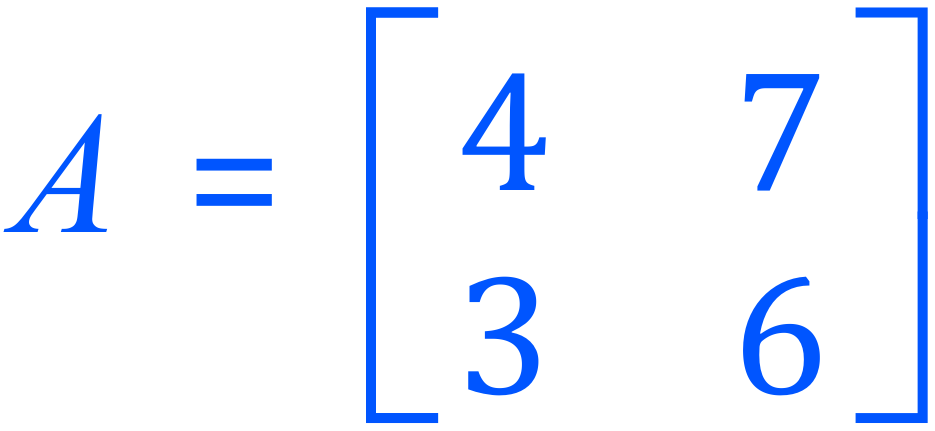
Step 1 - First of all we should see if the determinant is zero or nonzero, should it turn out to be zero then of course there is no point in continuing:
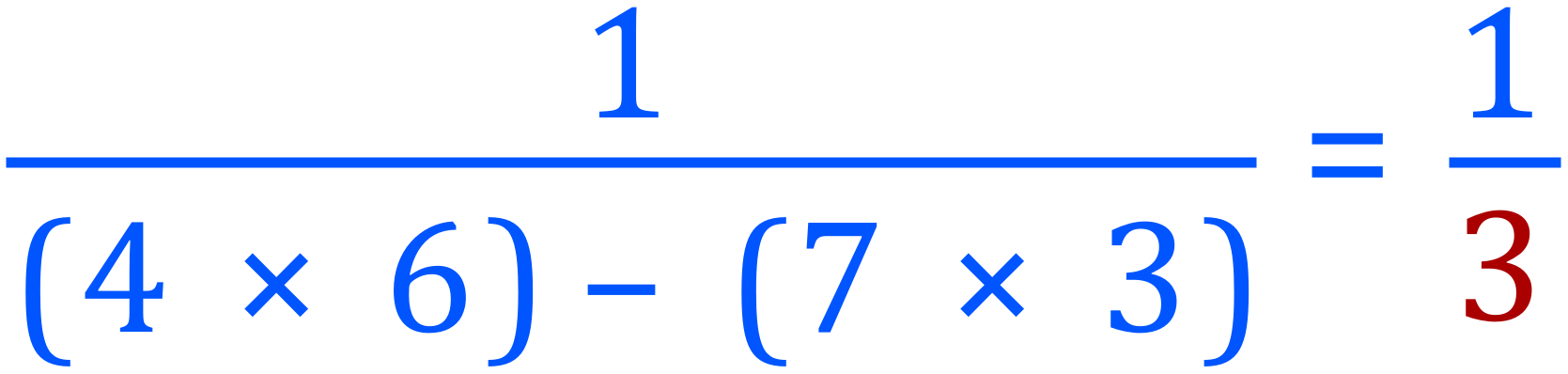
We can see that the determinant is nonzero (3), therefore the matrix A is invertible. Now we carry on with the formula:
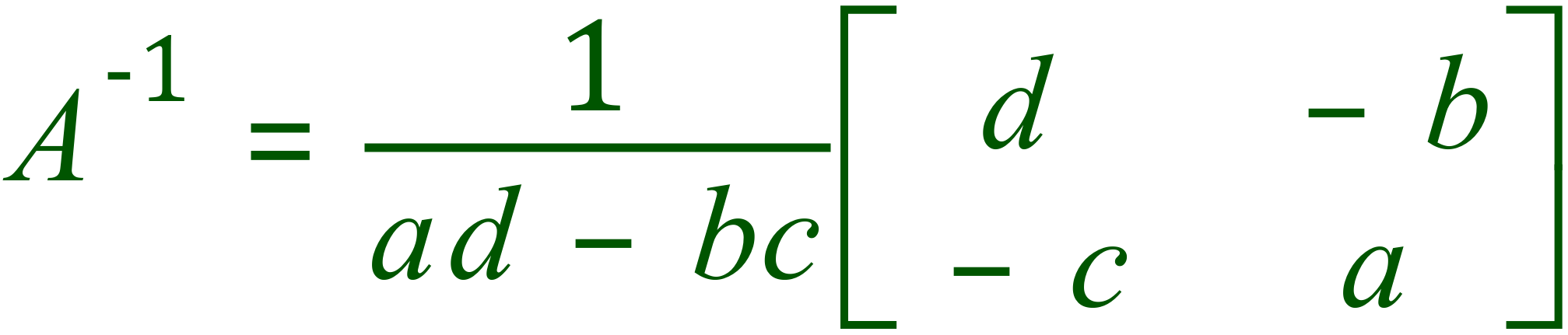
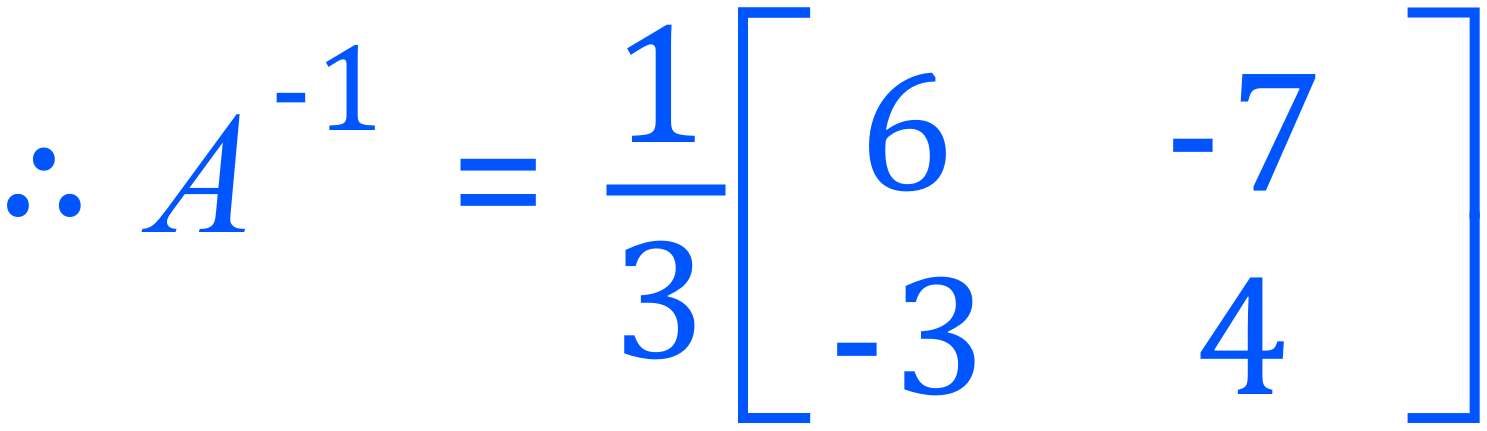
We calculate the product matrix as we would for any other multiplication (Using multiplication by a scalar, in this case one third):
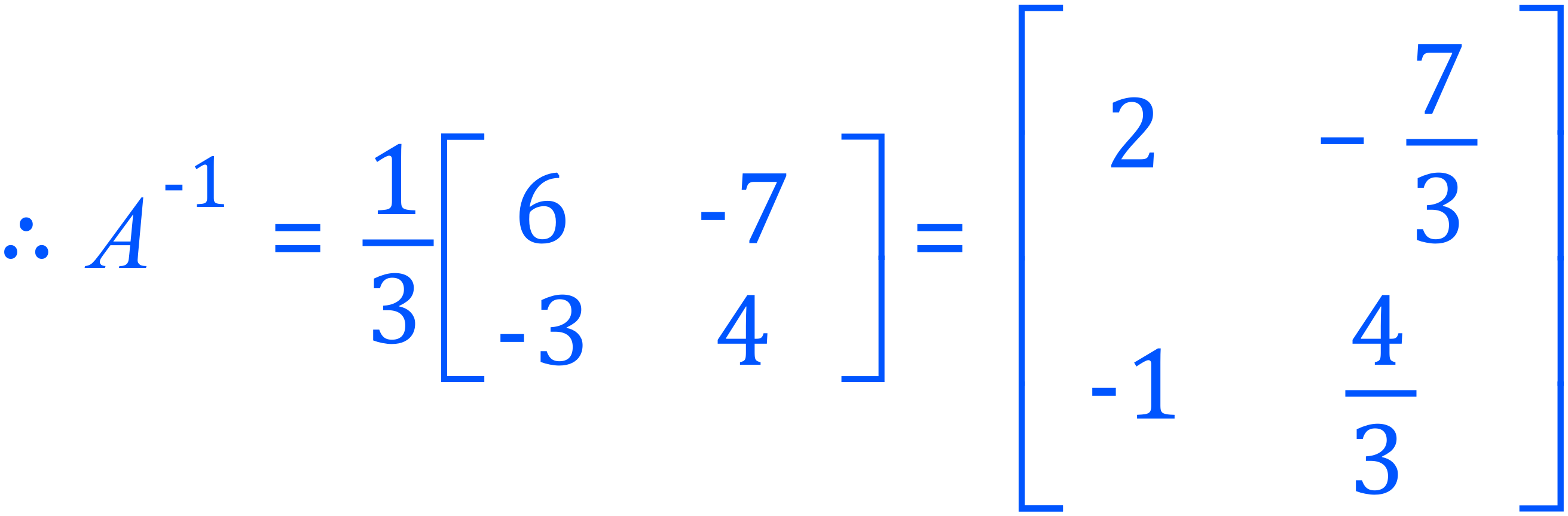
So, our inverse matrix is as shown, but how do we know this is correct? If we multiply a matrix by its own inverse we should obtain a product matrix known as the "identity" matrix. The identity matrix is a square matrix with a row of "1" diagonally from top left to bottom right, every other element is "0".
If we multiply our original matrix by the inverse we should arrive at the identity, if we do not then something has gone wrong.
Checking:
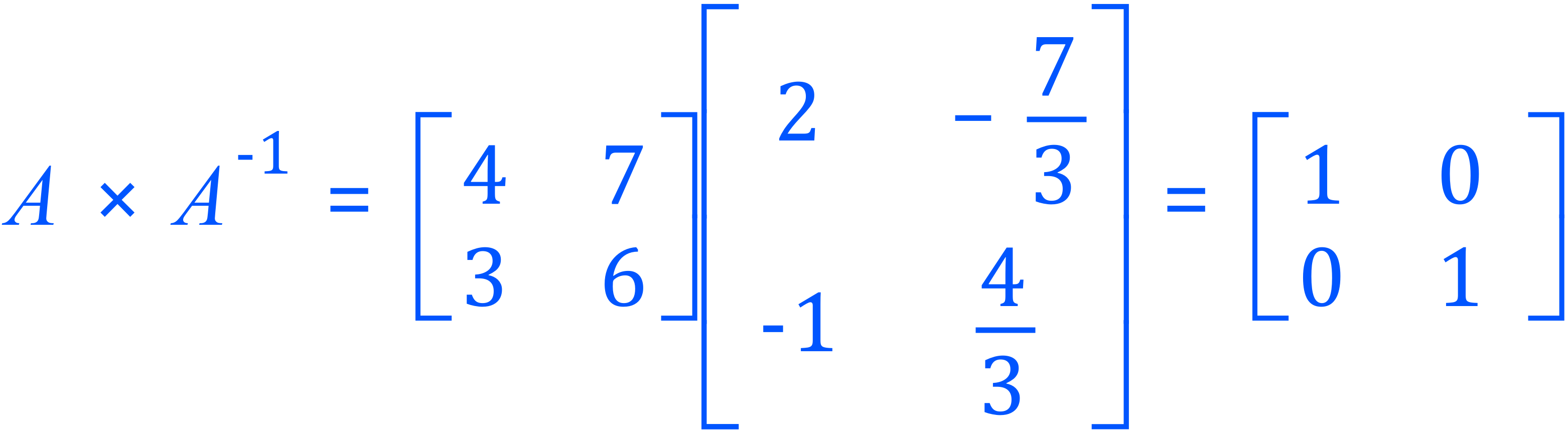
>> Questions <<
