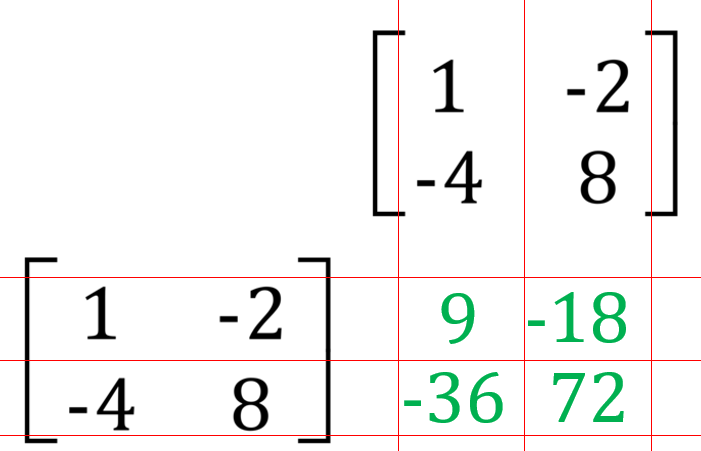
"Squaring" a Matrix
The square of a matrix, in its definition is the same as a square of an arithmetic number. The square of an arithmetic number (for example an integer) is the product of the integer multiplied by itself. This is basic arithmetic and hopefully very well understood.
Take the following matrix:
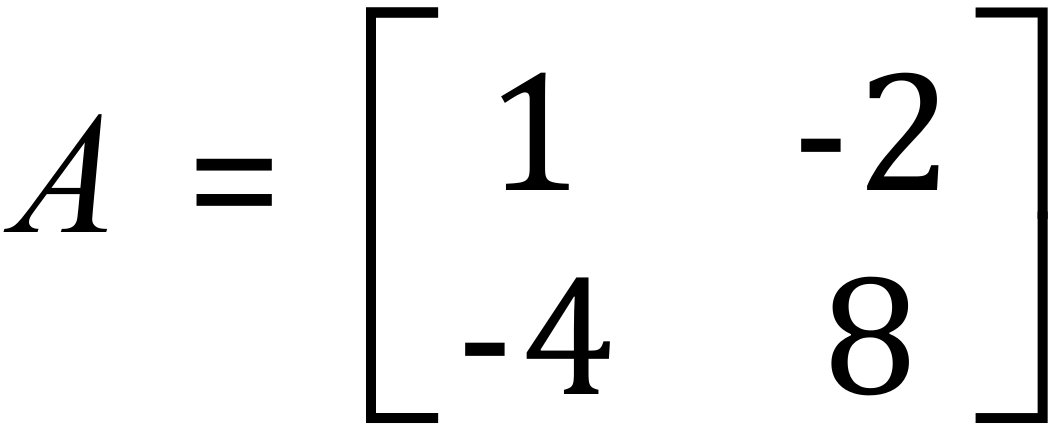
You will not be surprised I am sure that the square of the matrix can simply be written A2 . Naturally we would therefore write down:
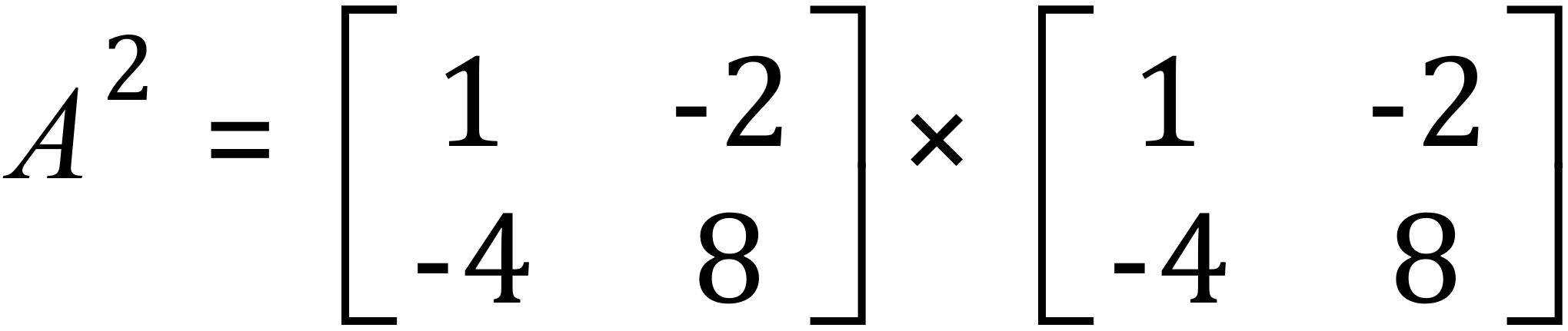
We would then perform the usual rules of matrix multiplication to establish the product matrix. If you recall the rules with regard to matrix multiplication you will remember the two matrices can only be multiplied together if the number of columns in the first matrix is equal to the number of rows in the second matrix.
With this in mind you can see that the squaring of this matrix can be performed because the number of rows in matrix A and the number of columns are the same, not only that but you can also conclude that the product matrix would be 2×2.