Inequalities
By now we should all know what an equation is, two separate sides of an expression with (somewhere) in the middle an "equals" sign:

Using some familiar tips and tricks, we can deduce from the above that the value for "x" is 3. We do this in stages, first of all we subtract 4 from both sides and in this particular example, that's as far as we have to go.
Let's take a look at a little bit more complicated example:
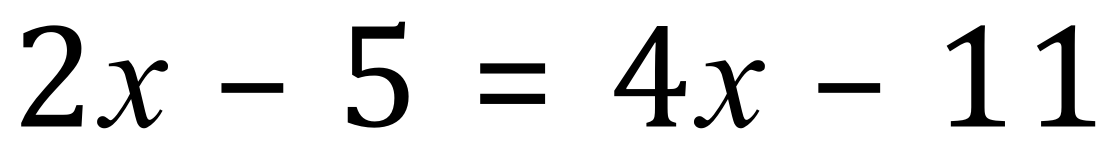
To try to establish a value for "x", we have to "isolate" terms including "x" on one side or other of the equation. In the above example the simplest thing to do to start with would be to
1. Subtract 2x from both sides:
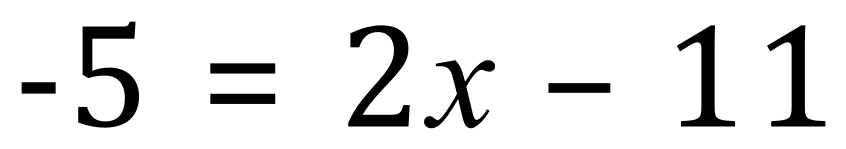
2. Add 11 to both sides:
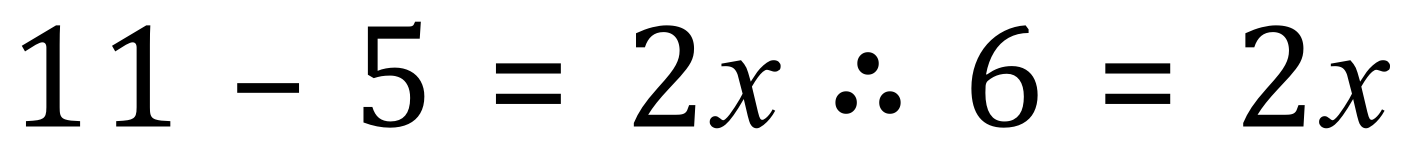
3. Divide both sides by 2:
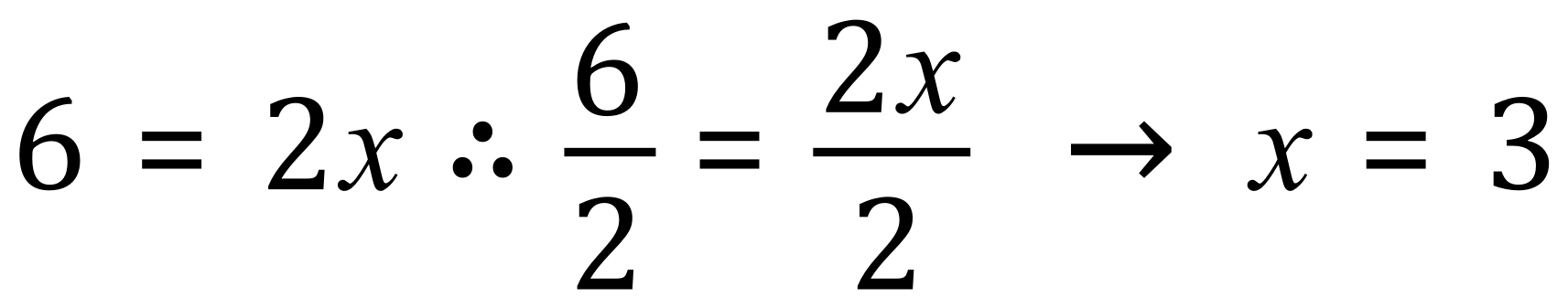
Although I appear to have made a meal out of this fairly simple equation, I have done this for a reason. When we start looking at "inequalities" we will use the same techniques as shown in the steps above to reduce expressions to a more manageable format.
So, what exactly do we mean by an "inequality"?
Well, I suppose you could look at it as "an equation that isn't an equation!"

In the above example, if the "greater than" sign was in fact an equality, we would be able to work out quite quickly that the value for "x" would be 2, however because we are saying that x +3 is greater than 2, the value for x cannot be any one particular fixed value.
To establish what "x" will in fact be, we apply the same rules as we did above. We try to isolate "x" on one side or the other of the equality. Let's start by subtracting 3 from both sides of this inequality:

The inequality value for "x" has to be correct, if for example you were to say that x = 2 then the inequality could not be correct. If this were the case (x = 2) then the result of the left-hand side of the inequality would be 5, and 5 is not greater than 5 so the inequality fails. If we say that x = 3 (i.e. it is greater than 2 as the end result would explain) then the left-hand side of the quality becomes 6, which is indeed greater than 5 and so the inequality is proven.
This might sound very complicated, it isn't. Apart from a few quirks when we start looking at using negative numbers, inequality problems aren't really that much more complicated than simple algebraic equations. Let's take a look at another example:

Use the same set of rules to reduce this inequality so that we end up with "x" on one side. First of all let's add 3 to both sides:

Now, if we divide both sides by 4, we will end up with a value for "x":
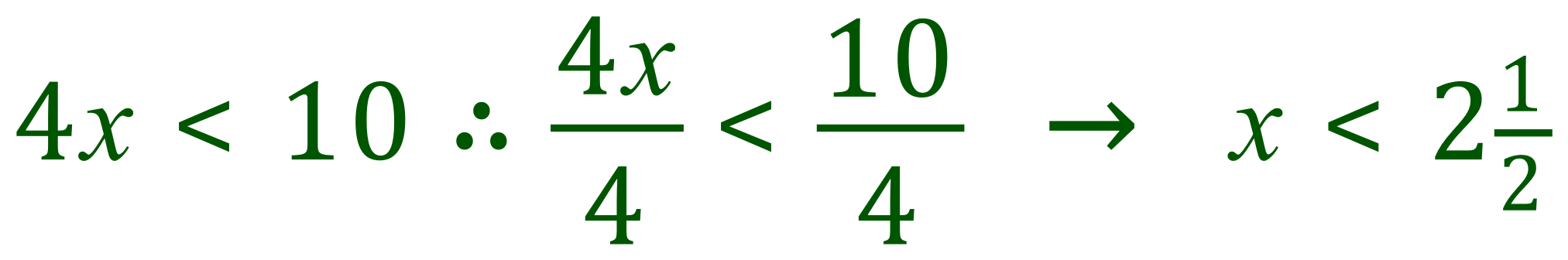
If we apply any value to "x" which is less than 2.5, we will see that the inequality holds true. If we suggest that "x" is equal to 2.5, then 4x would become 10, the inequality would fail because 10 cannot be less than 10.