Long Division with Decimal Numbers
As you have seen, Long Decimal Multiplication as I have chosen to call it is not really that much different to Long Multiplication in general, with a few tweaks and a few tricks we can multiply decimal numbers together as easily as integer numbers (that is, whole numbers). Long Decimal Division is, by the same token, and using similar tricks, just as straightforward as its counterpart Long Division. This part will show the tricks in action and enable you to divide what would appear at the beginning to be quite difficult numbers into each other.
Example 1
This apparently horrifying question asks us
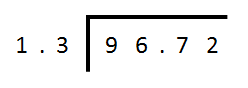
“how many 1.3’s go into 96.72? Now, normally you would reach straight for the calculator but you can do this quite simply by in if you follow the rules.
Step 1 - make a note of the number of decimal places in the dividend (that’s the 96.72 bit) and make a note of the number of decimal places in the divisor (that’s the 1.3 bit). These values set your ‘X’ and ‘Y’.
Step 2 - in just the same way that you did before in the long division questions, perform a long division of “how many 13’s in 9672?”:
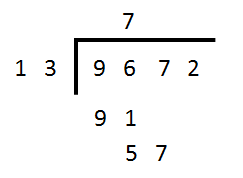
7×13 = 91, we take away the 91 from 96 which leaves 5 and bring down the 7 to make 57?
Step 3 - “how many 13 in 57?”, Well the answer this times 4 because 4x13= 52. We take the 52 from 57 leaving 5 and we bring down the remaining number which is 2.
Having brought down the 2, we are now left to the final step “

how many 13’s in 52?”, And the answer this time is an exact ‘4’ because 13 x 4= 52.
This time we are left with the 0 remainder so we know that we have finished the question, or have we?
If you cast your mind back to Long Decimal multiplication you will remember that we added together the number of decimal places of both numbers being multiplied together and we called them ‘X’ and ‘Y’. The total of X and Y gave us a number which was the number of decimal places that the answer had to be stated to.
It is slightly different when it comes to Long Decimal division, we call the number of decimal places in the divisor ‘X’ (1.3 in this case) and the number of decimal places in the dividend ‘Y’ (96.72 in this case). We subtract X from Y and the number that we are left with is the number of decimal places that we must quote our answer to (but see later, ‘Y’ is NOT always fixed, if the answer is becoming irrational, the dividend will be enlarged and more divisions will take place).
Let us reconsider our original sum:
Our divisor is 1.3 (one decimal place equals X) and our dividend is 96.72 (two decimal places equals Y)
Y minus X equals 2-1 = 1 so our final answer (whatever that may be) must be quoted to one decimal place.
Now let’s look at the finished sum:
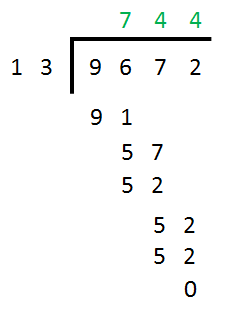
You can see that the decimal points are missing in the sum, but now it’s time to put them back.
As we said before Y minus X equals 1 so we must quote our answer of 744 as 74.4
Therefore:
96.72 ÷ 1.3 = 74.4
And this is our final answer.
Example 2
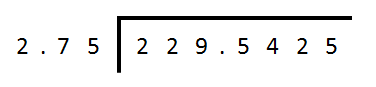
The next example will be a little bit more complicated, let’s take a look at it below:
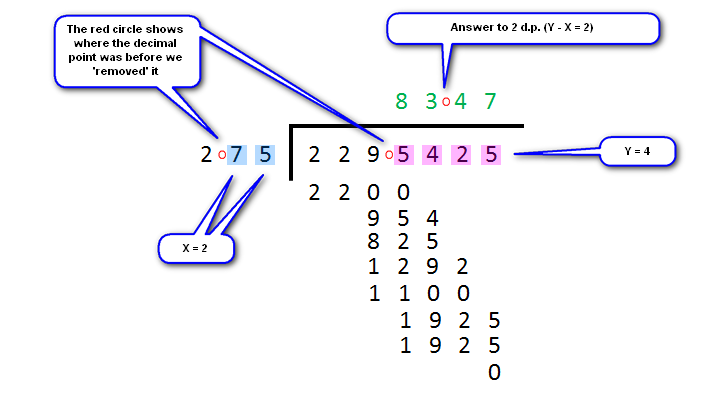
229.5425 ÷ 2.75, or “how many times does 2.75 go into 229.5425?”
Remember, our divisor X is 2.75 and shows two decimal places and our dividend Y shows four decimal places, so our final answer must be displayed to Y minus X or 4 - 2 = 2 decimal places.
Okay, let’s start the calculation:
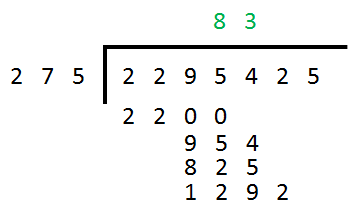
Step 1 – “how many 275’s in 2295?” – Trial and error here with a number of potential “Long Multiplications”, start at 9 and see what happens.
275 x 9 = 2475…..too big, try 8
275 x 8 = 2200….just right, so put ‘8’ above the 5 of 2295 on the answer bar, deduct 2200 from 2295 and bring down the 4.
Here’s what it will look like at this point:

Step 2 – “how many times does 275 go into 954?” – try 4:
275 x 4 = 1100, way too big so try 3:
275 x 3 = 825….this is the one…so put a 3 to the right of the 8 in the answer bar, subtract 825 from 954 and bring down the 2:
Step 3 - we have to make another guess now, this time “how many times does 275 go into 1292?”, Well we took a guess in step 2 that 275 times 4 is 1100, quite obviously if you added a further 275 to 1100 it would be too big for our purposes (1292) so we can guess at 4 this time. We put the 4 next to the 3 in the answer bar, subtract 1100 from 1292 and then bring down the 5.
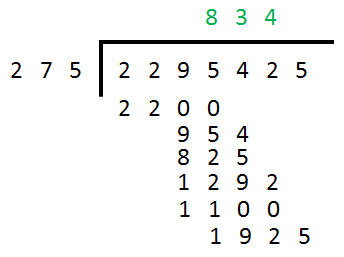
Step 4 - one final question “how many times does 275 go into 1925?”, Well in fact this question has been deliberately engineered so that the divisions don’t have to keep on going. The answer this time is 7 because 275 × 7 = 1925.
We put a 7 to the right of the 4 in the answer bar, we take 1925 away from 1925 leaving 0 and we have now finished except… We have to insert the appropriate number of decimal places to make the answer correct.
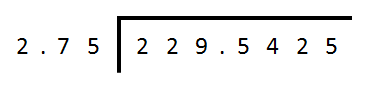
If you remember, this was the original question:
And we have come with our answer of 8347.
The divisor has 2 decimal places (remember X?) And the dividend has 4 decimal places (remember Y?), So Y minus X equals 2, therefore our answer is in actuality 83.47.
Just one point on the ‘X’ ‘Y’ method, is it can easily be proven by looking at further examples.
3 more diagrams shown below show the decimal places of the divisor and the dividend and it can easily be worked out what the ‘X’ and ‘Y’ values would be in each case.
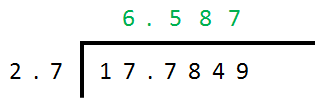
'Y' = 4, ‘X’ = 1 and the number of decimal places that the answer must be quoted to is 3 as shown.
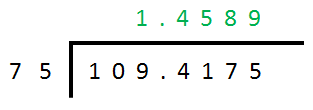
‘Y’ = 4, ‘X’ = 0 and the number of decimal places that the answer must be quoted to is 4 as shown.

‘Y’ = 2, ‘X’ = 1 and the number of decimal places that the answer must be quoted to is 1, as shown.
In all of the examples I’ve used so far, the answers have been deliberately engineered to be “finite” meaning that your divisions would not go on forever (and as a result, the value for ‘Y’ would be fixed). When they do, you have to decide how many decimal places you need to work to and this will be determined by the number of decimal places you are asked to quote your answer to (and this will subsequently have an effect on the value of ‘Y’, because the more decimal places you have to quote to, the larger ‘Y’ will become).
When you are conducting a long division, and the answer appears to be “infinite” you will of course run out of numbers to “drop down”. When this happens you continue to bring zeroes down until you have made at least one more calculation than the number of decimal places required, this will enable you to ‘round’ your number of decimal places accordingly.
(For each “0” you bring down, you make ‘Y’ incrementally larger by one, so when you have to decide at the very end how many decimal places to quote your answer to you will have to look at the final value for ‘Y’ and take it from there).
Okay then - in the next (and final) example I’m going to use a divisor and dividend which you will be familiar with when paired together. The dividend will be 22, and the divisor will be 7 and the answer to this will be a recurring decimal which is an approximation of the value of pi.
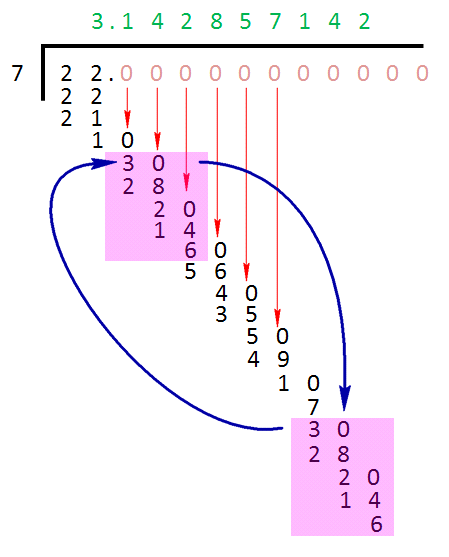
As you can see, this is a straightforward division into 22 by 7 but very quickly has to become a decimal long division, where the number of decimal places of the divisor never changes (it remains 0) but the number of decimal places of the dividend (22) constantly increases by 1 from 22, to 22.0, to 22.00, and so on forever.
The uniqueness about this particular example is that very quickly you will see that you’re dividing by the same numbers repeatedly, highlighted by the blocks of pink. This is what gives this particular approximation of pi it’s 6 decimal place recurrence of 3.142857.