So far we've looked at simultaneous equations where there are no powers of "x" greater than one, so in other words we have had no "x squared" components to deal with. Equations where there are no "quadratic" expressions are usually referred to as "linear" equations, so the simultaneous equations that we've been dealing with so far could perhaps be more properly regarded as "simultaneous linear equations".


In this section will take a look at the situation where we have "squared" entities to deal with. 


Take the following pair of equations:



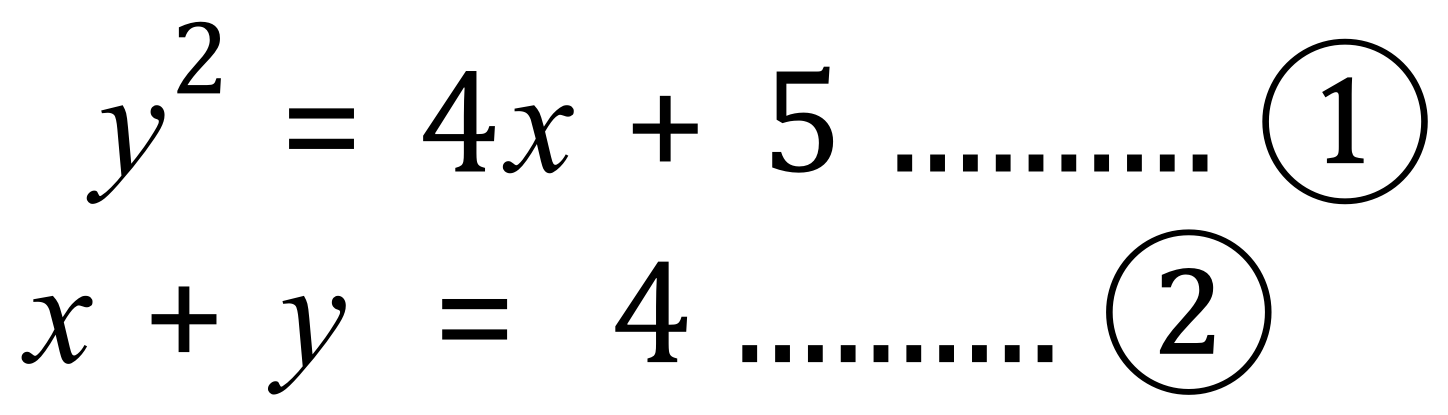
When solving these types of equations where one is quadratic and one is linear, we use a substitution method to arrive at a quadratic function. When we solve the quadratic function, as you would expect we return two "x" values, back substitution of these two values into one of the original equations will then return to "y" values, in other words these pairs of equations involve two sets of results.


Step 1 - Rearrange equation 2 so that it is then 'in terms of' "y" (make "y"  the subject of):



Step 2 - Substitute the newly translated equation (2) into equation (1):



Step 3 - Expand the newly substituted equation (1):




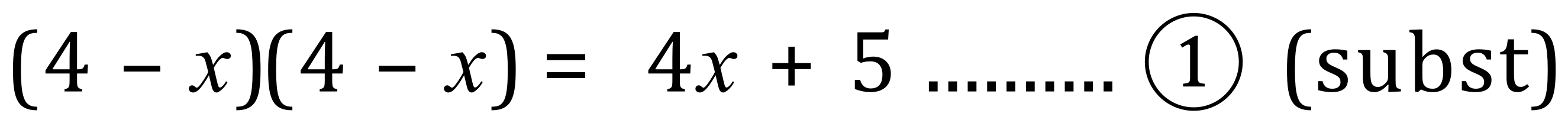
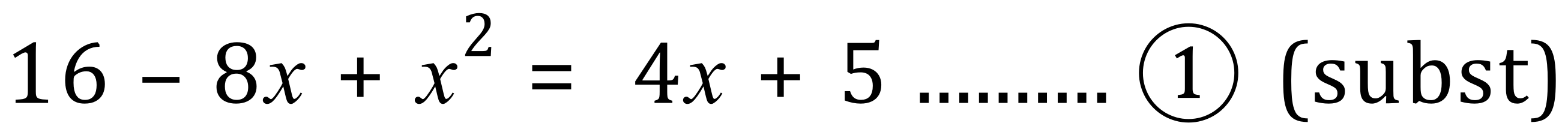
Step 4 - Collect all terms to the left, making an equation equal to ZERO, this is the first step towards making a recognisable Quadratic Equation:


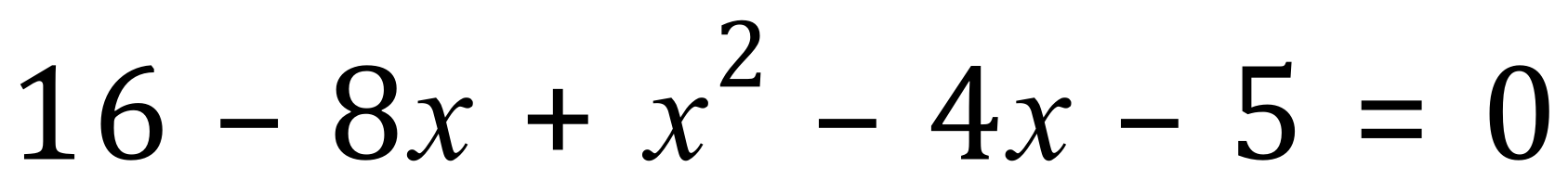
Step 5 - Tidy up and rearrange into a recognisable QE:




Step 6 - Use any suitable method to obtain the roots of this QE:



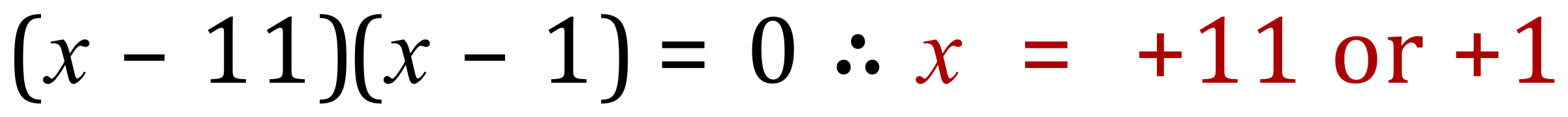
Step 7 - Substitute these values for "x" into (usually the simplest) original equation to obtain corresponding values for "y"



The PAIRS of values for "x" and "y" which satisfy the original equations are therefore:



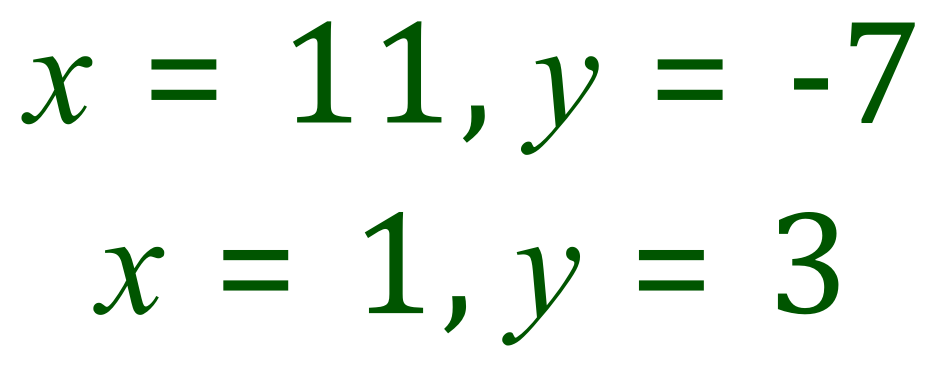
>> Questions <<