Using Matrices
At this particular point, unless you’ve already jumped about in the book and read the section on matrices you may not fully understand the next example. One of the main uses of matrices, or matrix algebra is to solve simultaneous equations and I will give you a quick example of it using one of the pairs of equations that we have used previously:
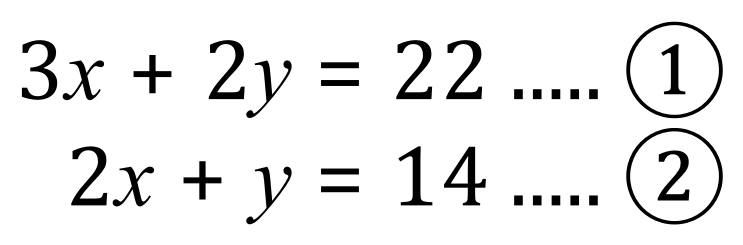
Converting the equations into “matrix form” will actually be explained more fully in the appropriate section, but I’m going to simply put these two equations into matrix form now and ask you at this point just to accept what I’ve done.
In matrix form then, our equations look like this (you can probably see why it looks like it does, and why the elements are where they are:
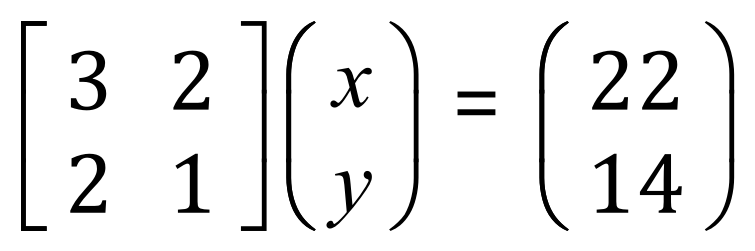
If you multiply out the matrices you will see that it does in fact give back the equations we started with, but as we haven’t presumably looked at matrices yet you probably won’t understand how to multiply them so just accept what I have put above.
BRIEFLY to multiply compatible matrices of 4x4 and 2x2 as in this example (I won't explain at this point WHY they are compatible):
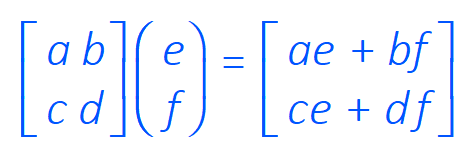
So, for example in the simple matrix problem:
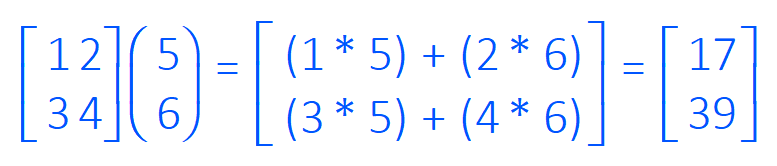
When we are looking at simultaneous equations in matrix form it is usual to refer to what we have put above in the following format:
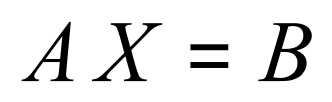
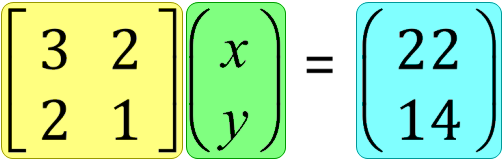
Where, I’m sure you can see the A refers to the matrix with the numbers 3 2 2 and 1 inside it and the X refers to the 2 element matrix ‘x’ and ‘y’, finally the B refers to the 2 element matrix with the numbers 22 and 14.
Given AX = B we can multiply both sides by the inverse of A, provided this exists, to give
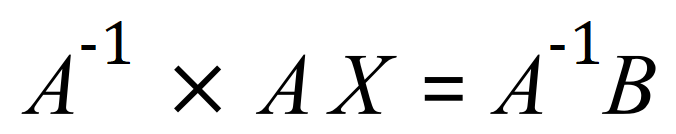
But as you will see when you study matrices, if you multiply a matrix by its own inverse you end up with a thing called the identity matrix, and the special feature about the identity matrix is that if you multiply it by matrix, you leave the value of that matrix unchanged.
Effectively, the meaning of the last 3 lines leads us to this:
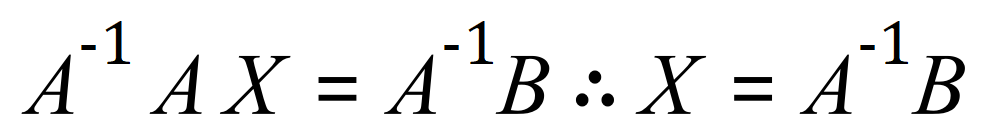
You must understand that I’ve missed out a lot of the rules of matrices in arriving at this expression because, as I said earlier, we have not yet covered matrices. When we do, you will find that there are a lot of idiosyncrasies, certain matrices cannot be multiplied together and certain matrices do not have an inverse.
OK we can leave the mechanics of matrix algebra to that particular section, let’s just crack on with solving the set of simultaneous equations:
Example 1
Step 1 - lets us rewrite our simultaneous equations in matrix form:
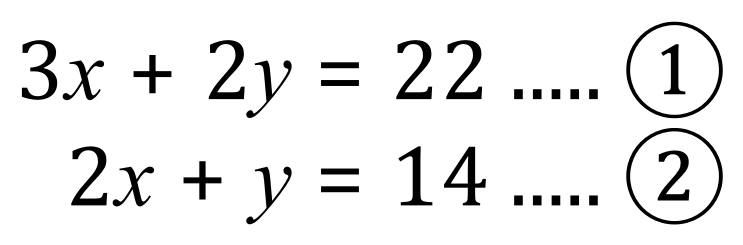
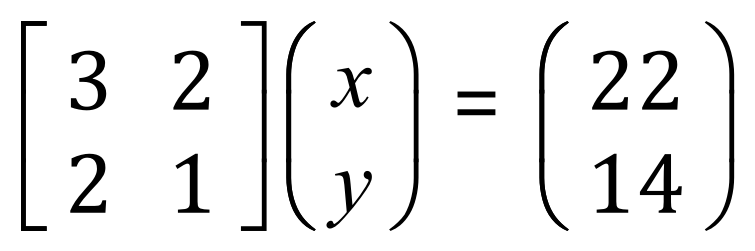
Using the rules of matrix multiplication you can in fact check at this point that you have your matrix correctly displayed.
Step 2 - Given that the formula for X is:
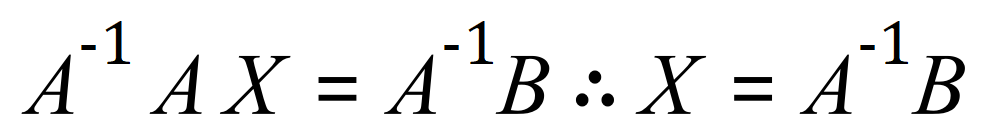
We need to evaluate the inverse matrix of A (A-1):
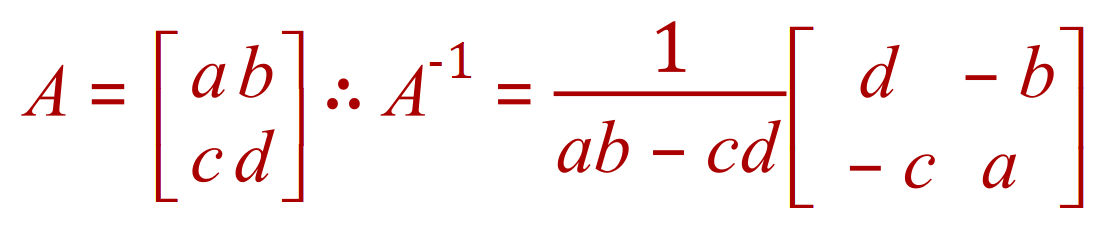
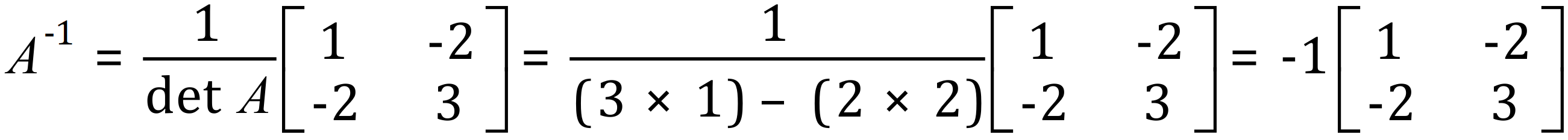
Step 3 - Therefore:
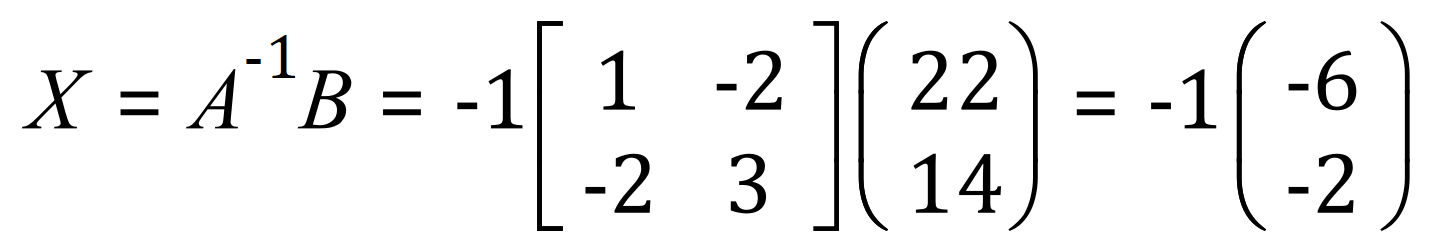
From this final result for X we can work out that ‘x’ = 6 and ‘y’ = 2 (choose either of your original equations and make substitutions to satisfy yourself that this is in fact correct).
Let’s take a look at another example:
Example 2:
Given the pair of simultaneous equations:
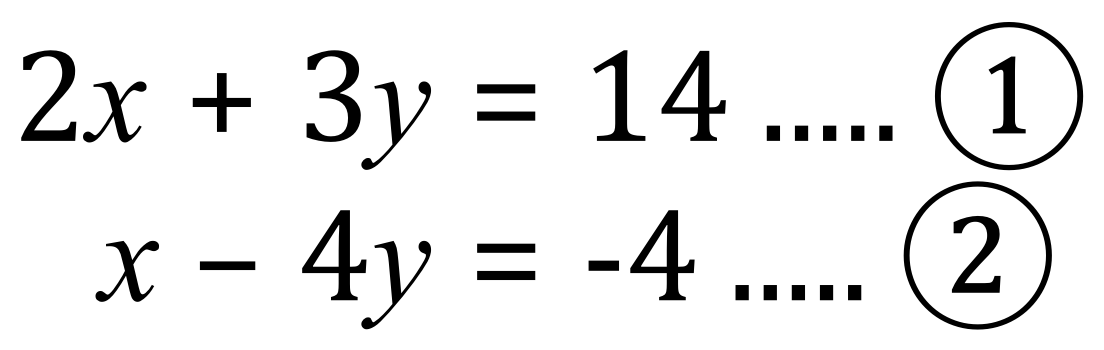
We can easily convert these to matrix form as follows:
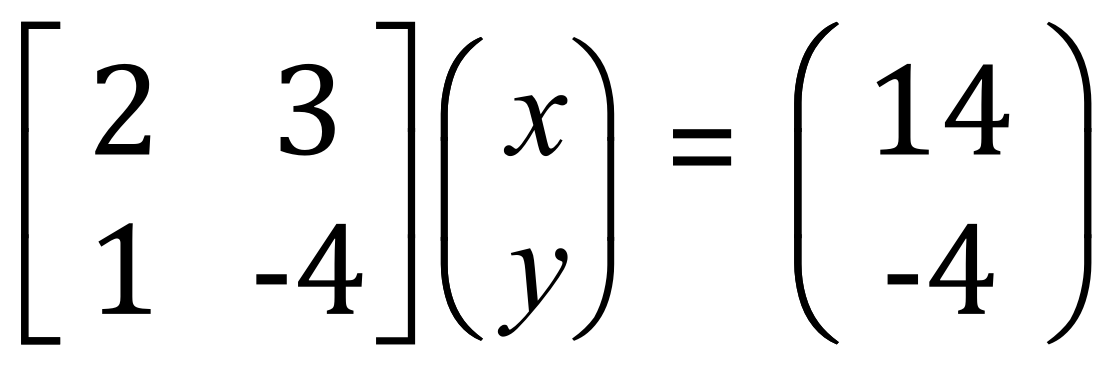
Once again we are given the formula for capital X:
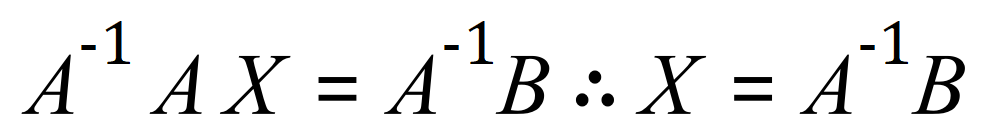
We need to evaluate the inverse matrix of A (A-1):
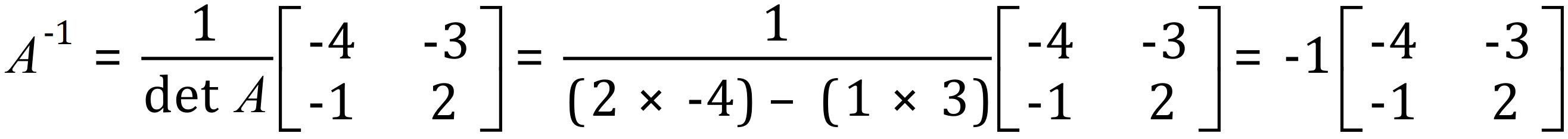
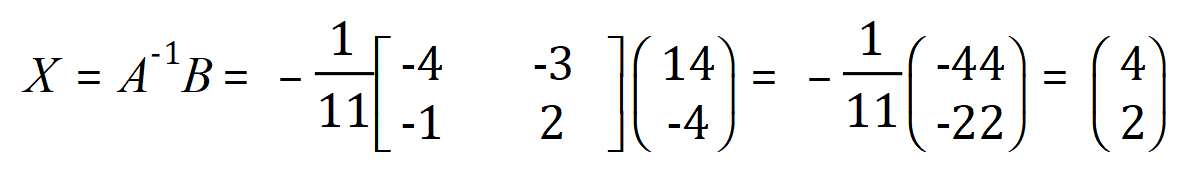
We therefore conclude that ‘x’ equals 4 and ‘y’ equals 2, against substitute these values back into either of the equations and you will find that this is correct.
Example 3:
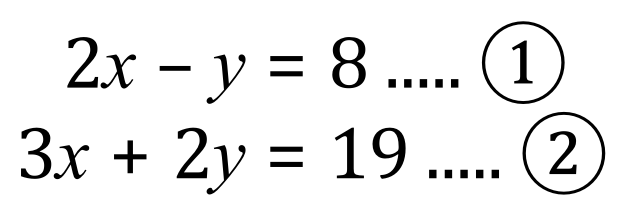
Following the rules of matrices, we create our matrix-representation of the equations thus:
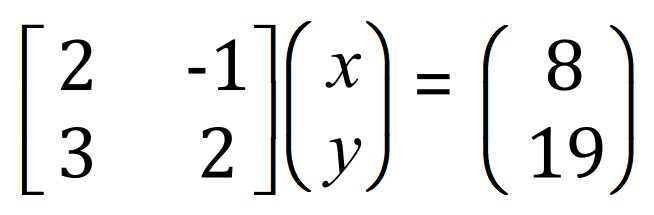
(remembering that -y is in fact -1y)
Given the matrix rules from above:
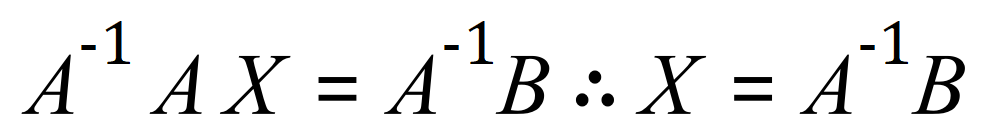
We now need to evaluate the determinant, and therefore the inverse matrix as before:
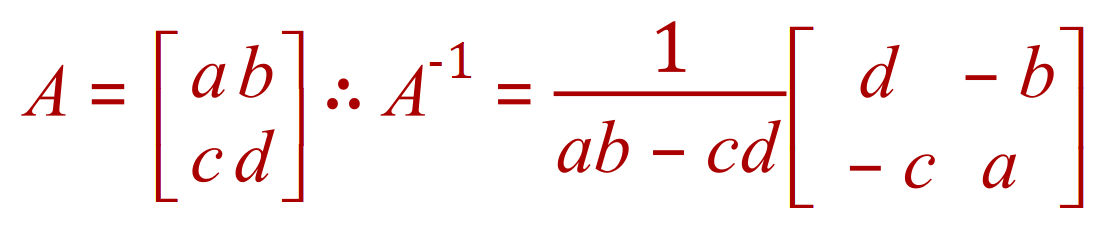
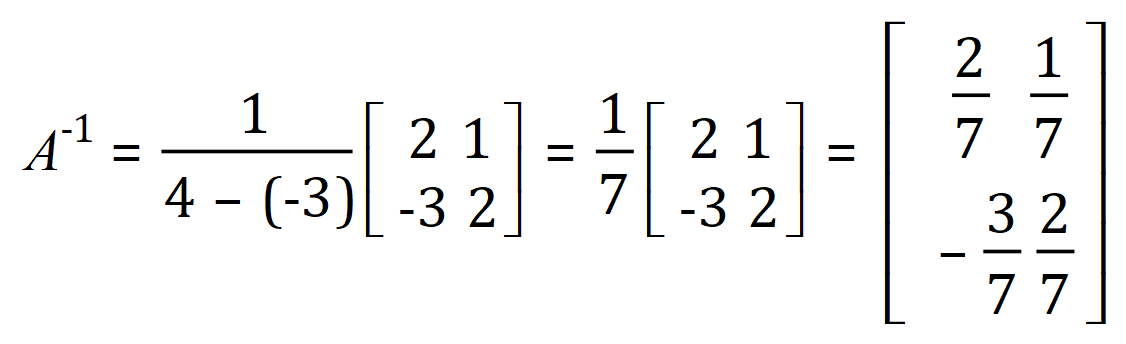
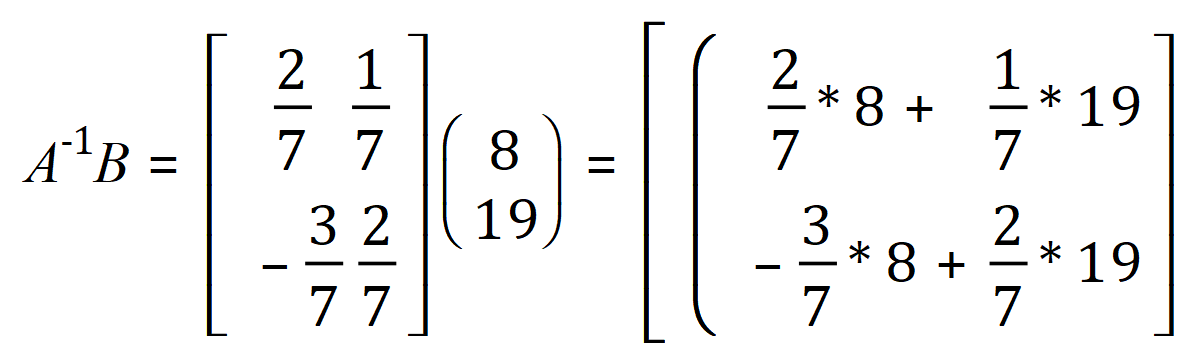
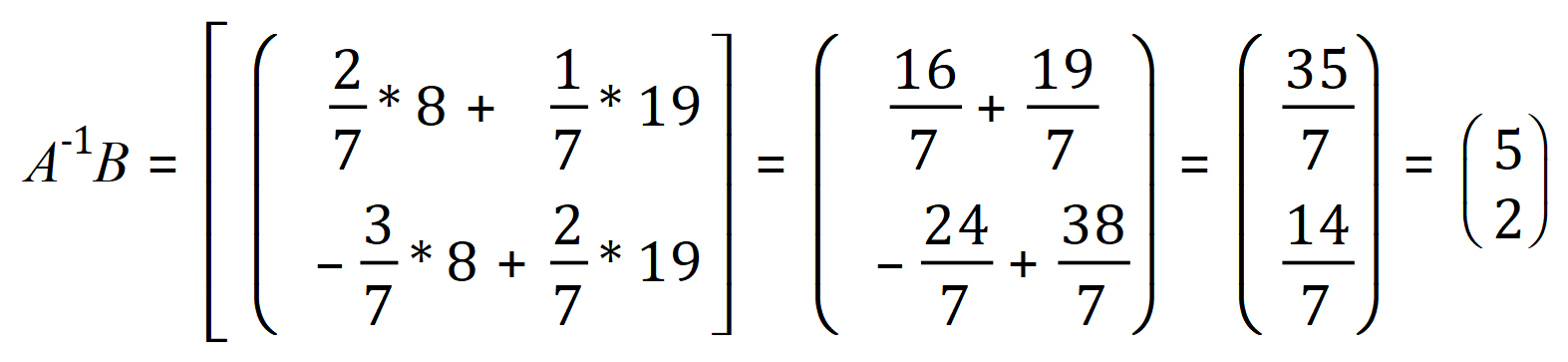
Therefore x = 5 and y = 2, substitute as before in either of the original equations to satisfy yourself that this is correct.
I would venture to suggest that the elimination method is simpler but I must admit I do enjoy the challenge of using the matrix approach.