Substitution
Q1. Using the substitution method, solve the below pair of Simultaneous Equations:
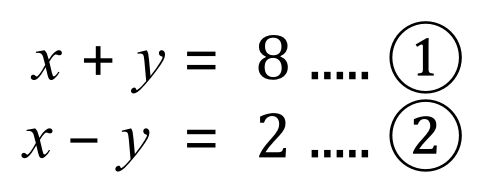
Let us and transpose it, making 'y' the subject:
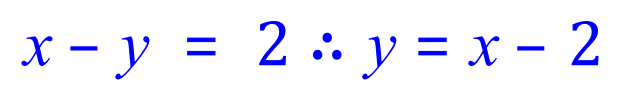
Substitute this newly transposed equation into equation 1:
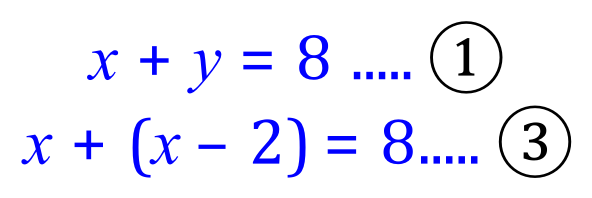
Tidying up equation 3:
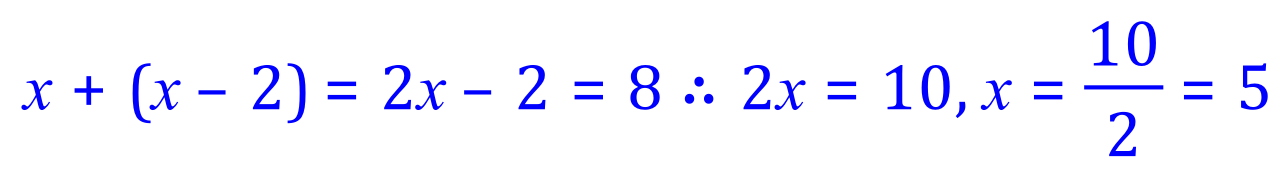
From (2):
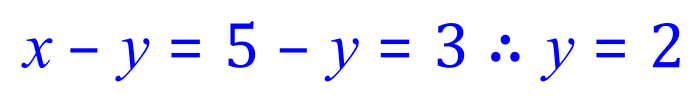
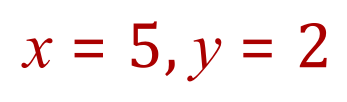
Q2. Using the substitution method, solve the below pair of Simultaneous Equations:
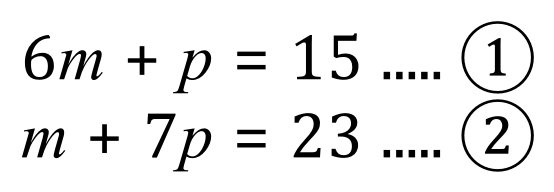
Isolate 'm' in (2) (transpose in terms of 'm'):
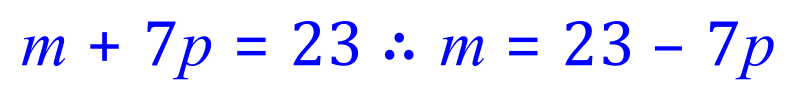
Substitute expression for 'm' into (1)
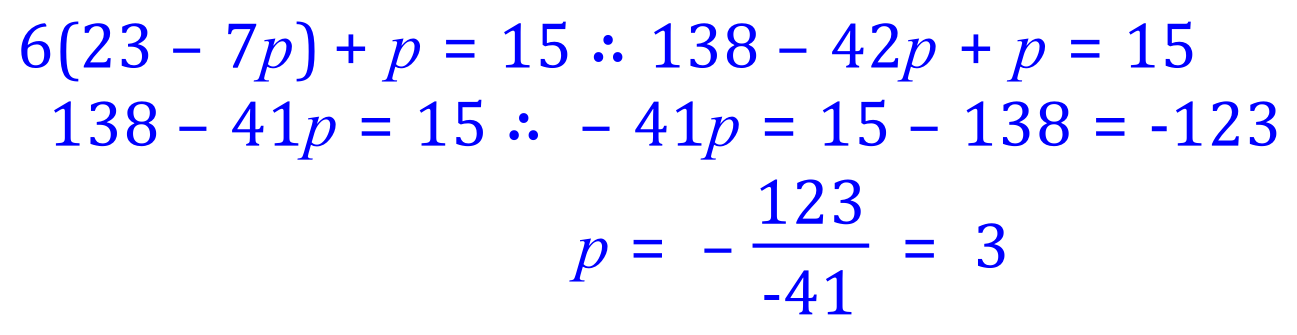
Substitute p=3 into (2)
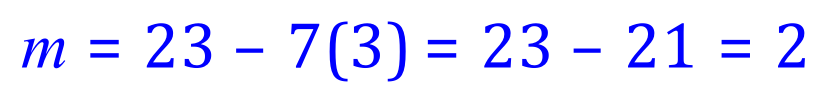
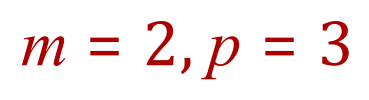
Q3. Using the substitution method, solve the below pair of Simultaneous Equations including a Quadratic function, determine BOTH sets of values which satisfy the variables 'x' and 'y'
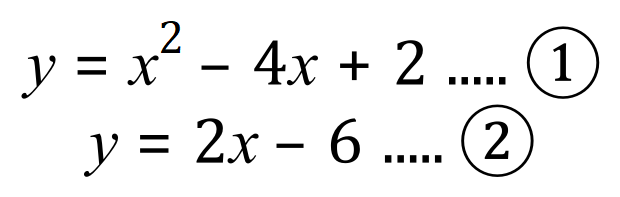
Substitute the value for 'y' in (2) into (1):
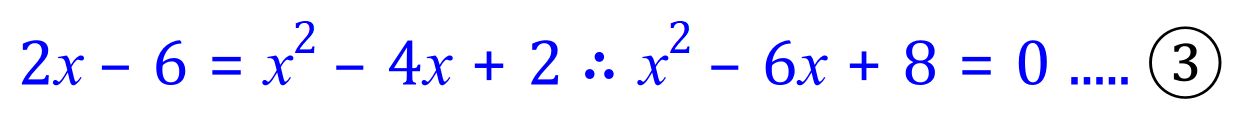
Solve the Quadratic Equation (3) to find the roots 'x':
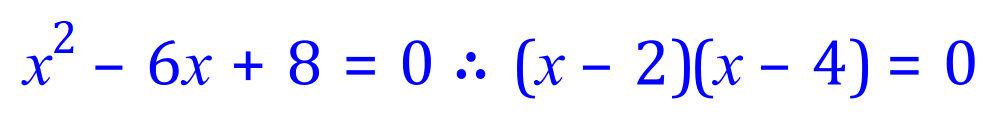
(Remember that using "inspection", we are looking for two numbers which ADD to -6 and MULTIPLY to +8, -2 and -4 will do this)
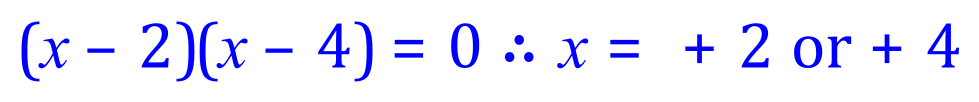
Now we need to substitute both individual values for 'x' into one of the original equations to find the corresponding values for 'y'. Equation (2) is the easiest choice:
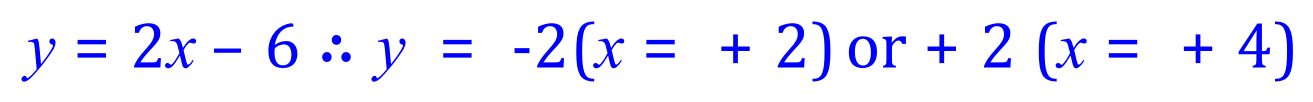
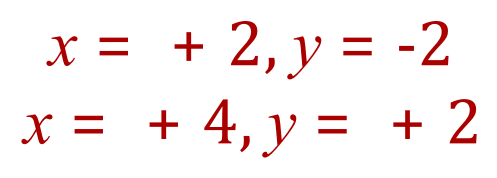
Q4. Using the substitution method, solve the below pair of Simultaneous Equations including a Quadratic function, determine BOTH sets of values which satisfy the variables 'x' and 'y'
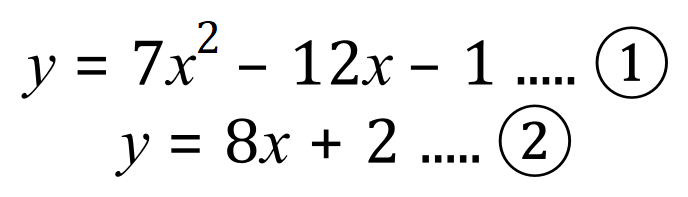
Substitute the value for 'y' in (2) into (1):

Solve the Quadratic Equation (3) to find the roots 'x':

(Remember that using "inspection", we are looking for two numbers which ADD to -20 and MULTIPLY to -21 ..... -21 and +1 will do this)
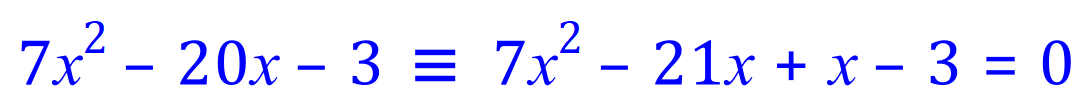
Factorising the right side of the above:
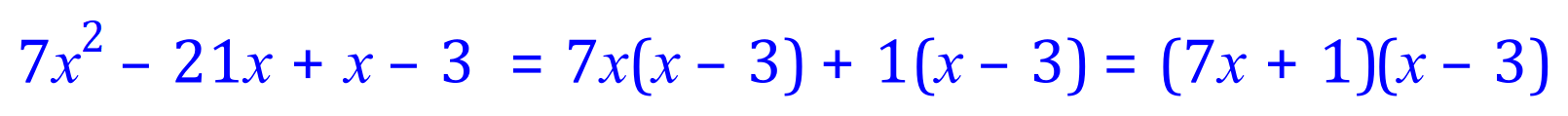
Looking at both sets of parentheses, the values of 'x' that satisfy the product quadratic are:
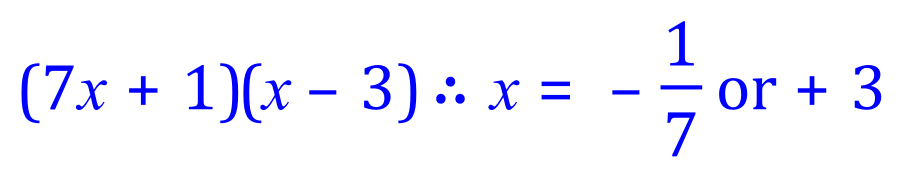
Now we need to substitute both individual values for 'x' into one of the original equations to find the corresponding values for 'y'. Equation (2) is the easiest choice:
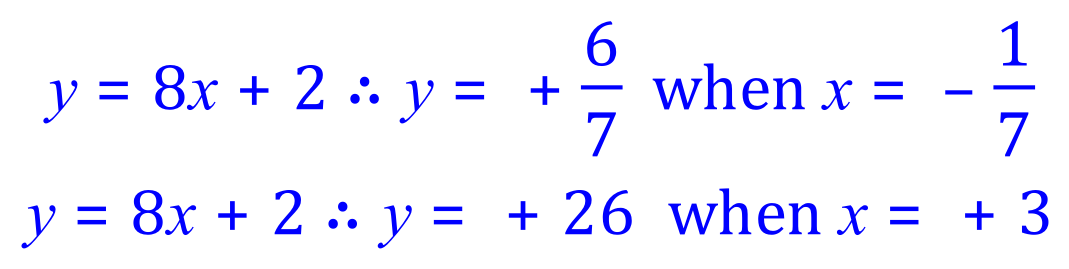
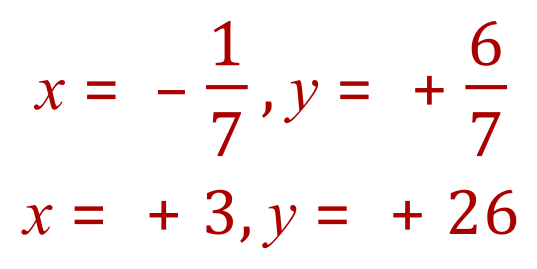
Back To >> Questions <<
Back To >> Simultaneous Equations by Substitution <<