In the previous section we saw how to obtain the first derivative of a simple function 'x' squared. However, what do we do if the coefficient of 'x' is not on?.


At this point we introduce the "Constant Multiple Rule".. We assign the letter 'a' (quite arbitrarily, we could use anything however maths books seem to favour the early part of the alphabet for constants and coefficients, and the latter part of the alphabet for variables). Let us know restate the equation from the previous page in terms of our newly arrived at constant multiple 'a':


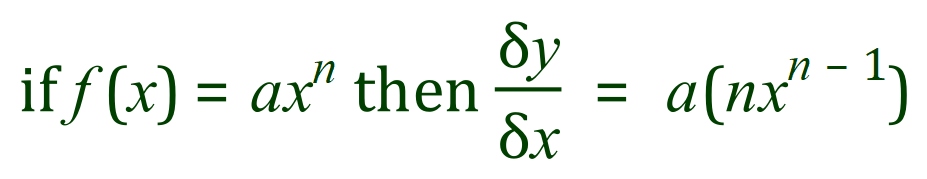
What we are effectively doing is taking the constant multiple to one side, differentiating what is left, and then bringing the constant multiple back into play:


Examples:








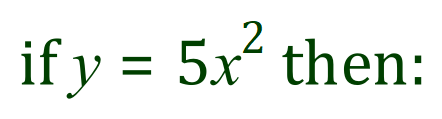
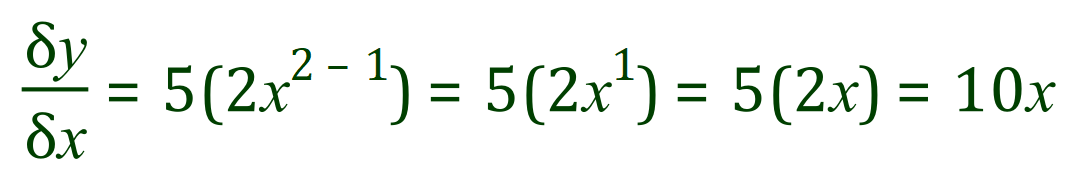
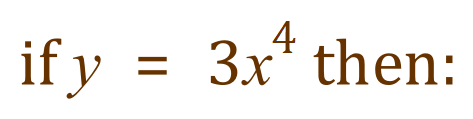
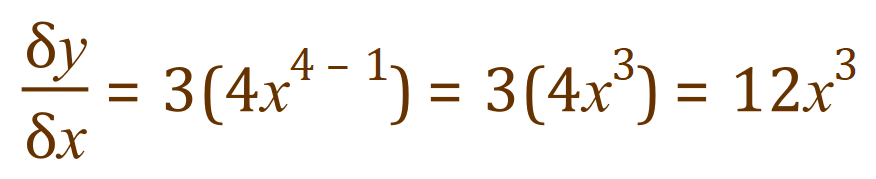
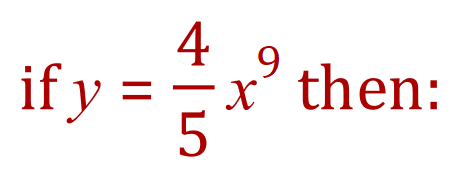
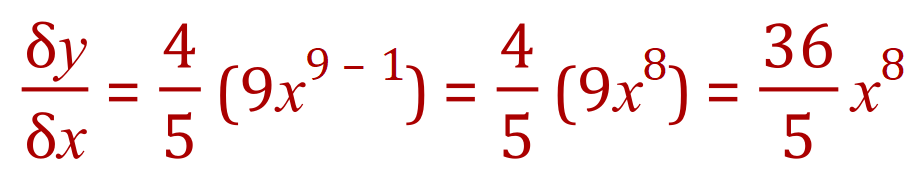
So far we have been dealing with very simple expressions, but what happens when we start adding expressions together? That is… we meet an algebraic expression involving the sum of two or more separate expressions such as:


 ?


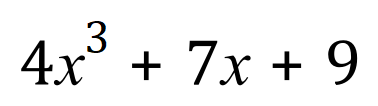How do we differentiate this? Well… This leads us to our next rule… “The sum / difference rule”



Go To >> Table Of Standard Derivatives And Integrals <<