The Sum / Difference Rule
This is quite a simple rule of differentiation which states that “the derivative of the sum of two or more functions is the sum of the derivatives of the individual functions”
So for example if we look at the expression we met earlier:

We can see that this expression is in fact the sum of three functions of ‘x’…….
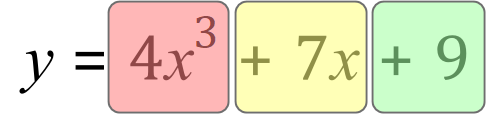
At the end, nine is a constant but if you want to be pedantic it is still function of ‘x’:
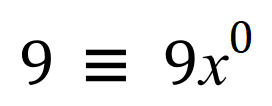
The derivative of this expression is this:
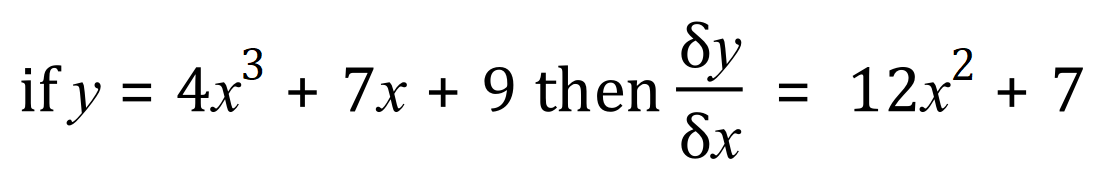
Or, more formally:
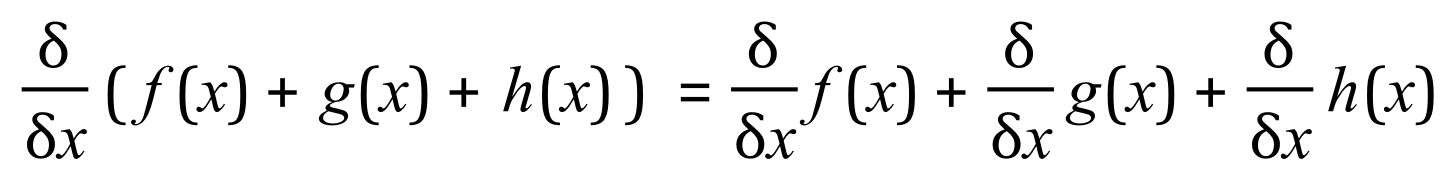
Just as an aside, why does the constant disappear when differentiated? Well take a look at the constant 9 above, but in its “more obvious function of x” format, which probably makes it a little bit clearer:
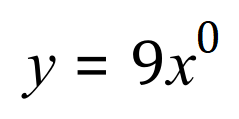
Apply the basic rule for differentiation which we saw earlier:
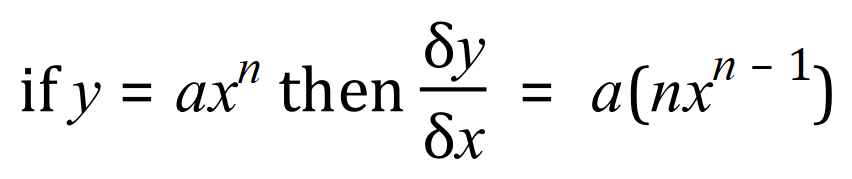
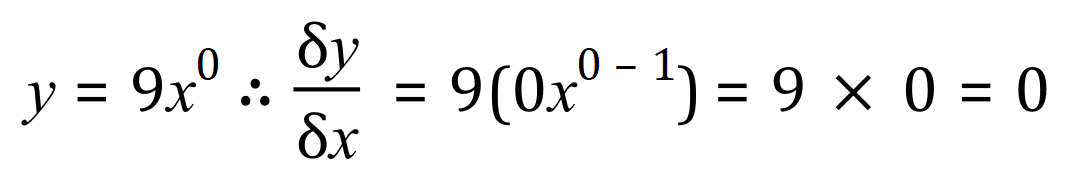
A clumsy way to demonstrate it because the somewhat complicated expression '0 to the power x-1' evaluates to 0 anyway so 9 of them is going to be 0 as well!
But hopefully you can now see why the constant disappears when differentiated and it is the same for any constant.
The sum / difference rule also applies when you’re subtracting, so if the expression previously had been this:

As you’ve probably found in mathematics anyway, addition and subtraction are always quite straightforward except in the case of subtraction which is not commutative:
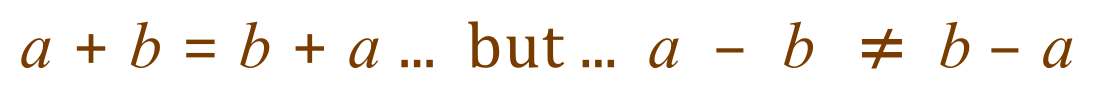
But when we look at calculus, and we start to multiply and divide it does start to get a little bit more complicated.
Go To >> Table Of Standard Derivatives And Integrals <<