The Ideal Gas Equation
Combining the gas laws of Boyle and Charles leads us to the Ideal Gas Law / Ideal Gas Equation:
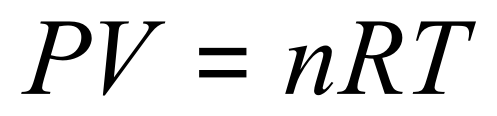
From Boyle's law we can see that pressure and volume are inversely proportional to each other, if you think of the simple example of a bicycle pump, if you press the plunger down to decrease the volume of the air inside the tube, you increase the pressure that the air exerts on the walls of the tube and the plunger.
So:
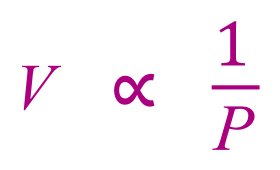
Similarly from Charles law we can see that volume is directly proportional to temperature, as many camper has probably found out to his or her mistake by heating up a can of baked beans on the campfire without puncturing the lid first!
So:

When we combine the laws, we reach an expression:
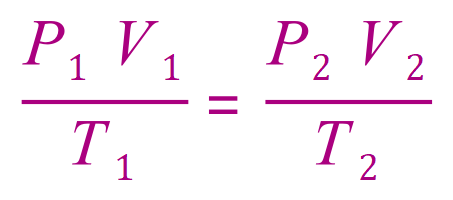
Further manipulation of the laws (which I won't go into here) leads us to what has now become known as the "Ideal Gas Equation".
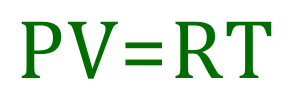
This equation summarises how an "ideal gas" would behave. In practice real gases do not behave "ideally" but the deviations are small enough as to be easy enough to disregard in the main. The gas constant "R" is a new concept for you, the "universal" or "molar" gas constant which is often given the value of 8.31 J per kelvin per mole.
Generally, the ideal gas equation will be written in the format:
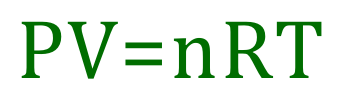
Where "n" takes into account the number of moles of gas under consideration.
More often than not, questions involving the ideal gas equation would come in the A-level syllabus, and it is usual to be given the value for the gas constant and 3 out of the remaining 4 variables, from which (yes, you guessed it) you will be asked to calculate the 4th value.
Q. Calculate the volume occupied by one mole of a gas at 25 oC and 100 kPa.
A. If you have any difficulties in transposing the ideal gas equation in terms of any unknown variable that you will be required to find, then you need to practice this as these are likely to be your "bread-and-butter" questions at this level. This particular question asks us for a volume, so we transpose the equation accordingly:
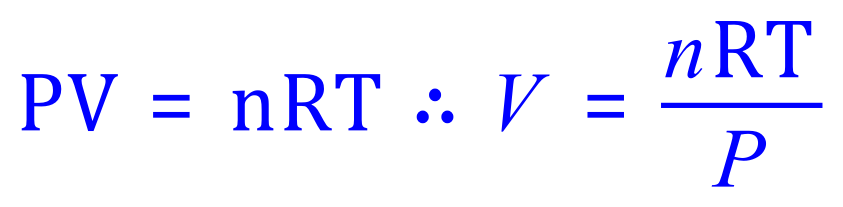
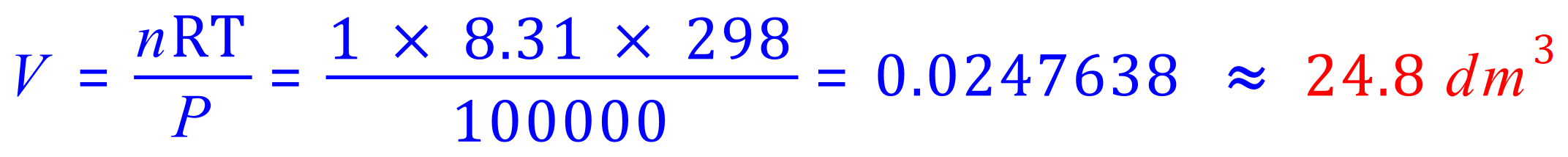
Remember your units here, P = Pa so you must convert 100 kPa to 100,000 Pa. V= m3 so your answer may be unrecognisable as a value in cubic metres, 24.8 dm3 or L is usually more recognisable. R is the Gas Constant in Joules per Kelvin per Mole (J K-1 mol-1).
Q.Calculate the relative molecular mass of a gas if a 500 cm3 sample at 20 oC and 1 atm has a mass of 0.66 g
A. This time we transpose the equation to find "n", the number of moles in the sample. From this we can calculate the Mr of the gas. 1 atm = 101325 Pa and you will normally be given this value, or be expected to know it (!).

Entering (converted) values:
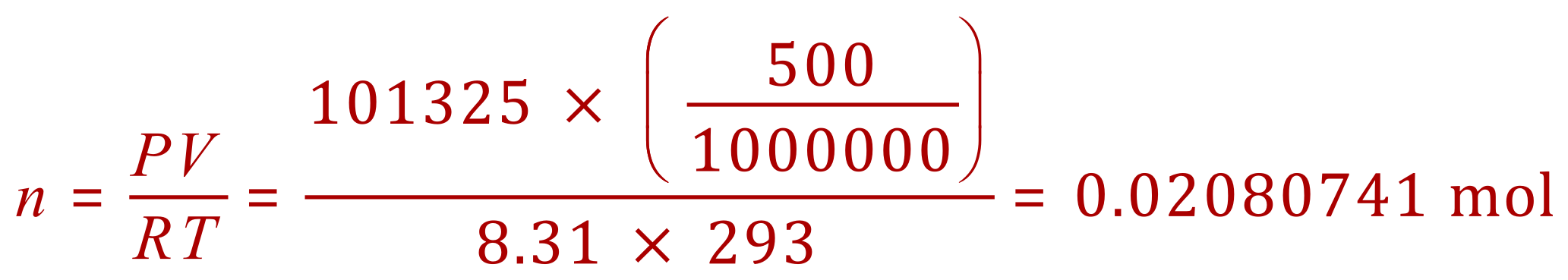
Our sample was 0.66g which is already in the correct units (gram), therefore if 0.02080741 mol has a mass of 0.66g then 1 mole has a mass of (and therefore a Mr):
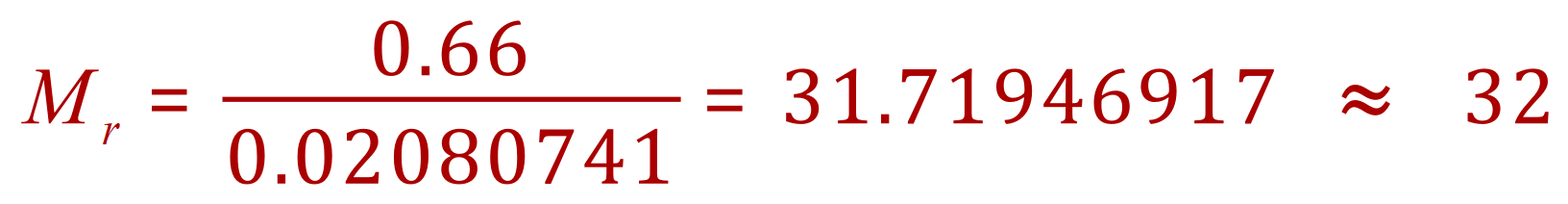
Q. At 25 oC and 100 kPa a gas occupies a volume of 20 dm3. Calculate the new temperature of the gas if
(a) the volume is decreased to 10 dm3 at constant pressure.
(b) the pressure is decreased to 50 kPa at constant volume.
A. (a)
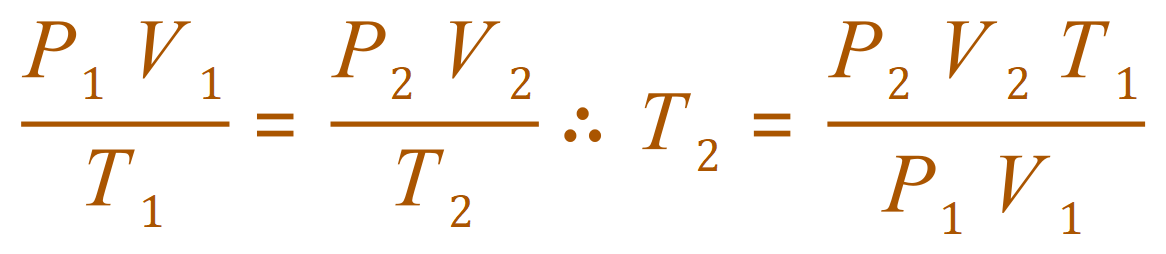
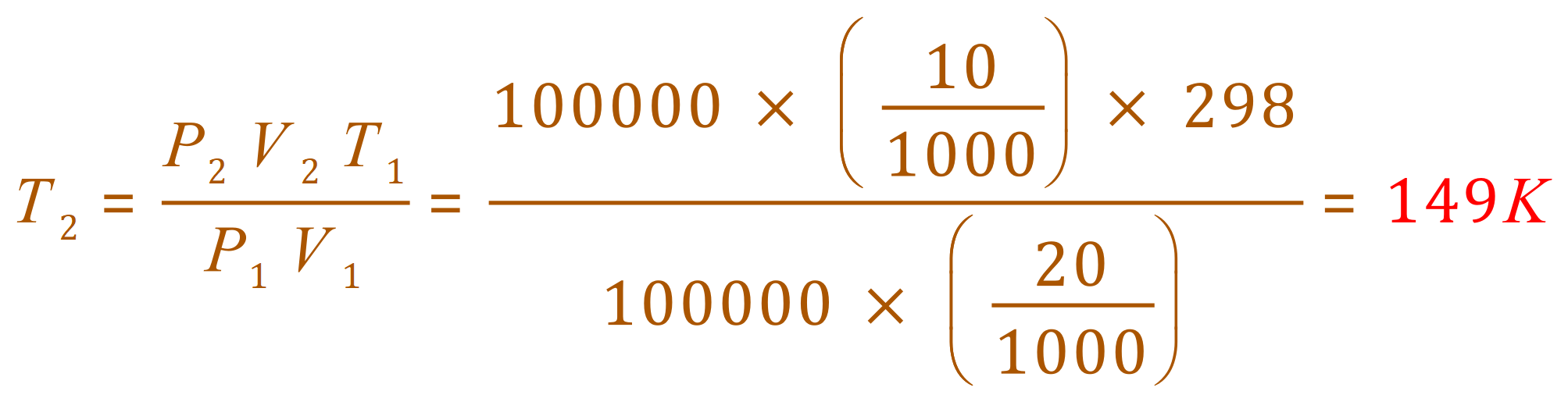
In fact this is a Charles Law example where the Pressure-Temperature proportionality rules could have been applied. Using the Ideal Gas Equation is acceptable but as the pressure has been kept constant, it is pushing you to Charles Law, also the 100,000 is an unnecessary complication in the calculation.
A. (b) This is a Gay-Lussac problem as we are told that the Volume is held constant:
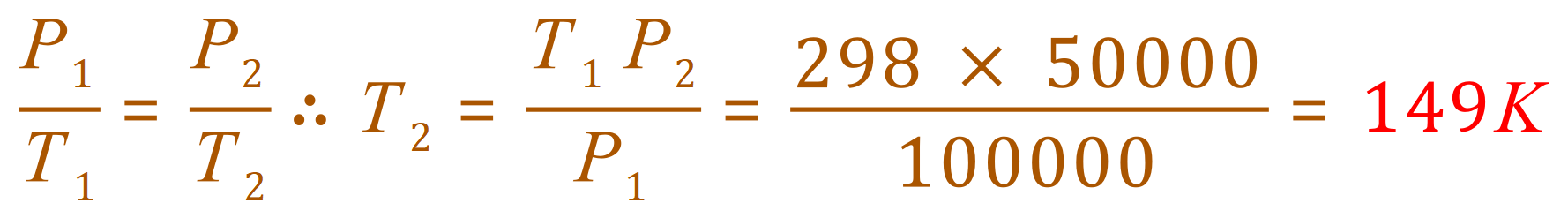
>> Questions <<