[A] Ideal Gas Equation and Moles
In all of the questions that follow remember your units:
Pressure equals Pascal = Pa
Volume equals cubic metres = m3
Temperature equals Kelvin = K
n equals moles = mol
R equals the gas constant = 8.31 JK-1mol-1
Q. 1.25 g of an unknown gas occupied 923 cm³ at a pressure of 102 kPa and a temperature of 290 K. Find the relative formula mass of the gas.
In all questions such as this, you need to keep a very careful eye on your units, which is why I've included all of the units at the top of the question page. In this particular question we are told that 1.25 g of the gas occupies 923 cm³ at 102 kPa, 290 K.
Consider the ideal gas equation:
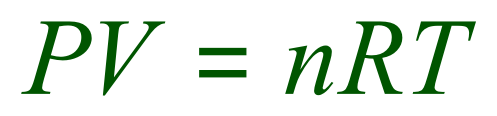
First of all, what are we being asked for? Well we are looking at a relative formula mass which has to come (in some way, shape or form, from the number of moles of the gas) so we are looking at a calculation involving the identification of the value of 'n'. We can see that this is the case because we are given values for the pressure, temperature and volume. The gas constant R will also be provided in a question like this.
Let us transpose the equation in terms of 'n':
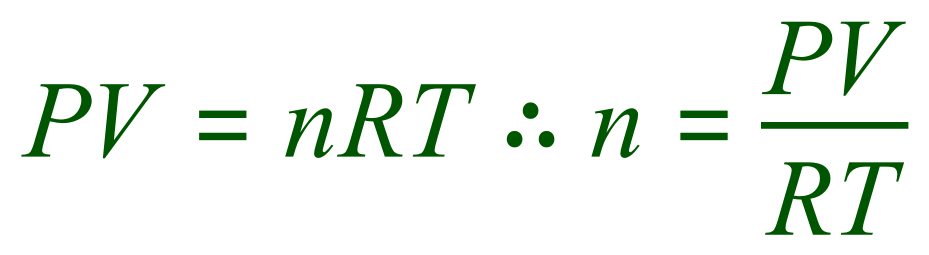
Before we "plug in" our given values, we need to make sure that they are all in the correct units. 923 cm³ needs to be converted to 0.000923 m³, 102 kPa needs to be converted to 102,000 Pascal, the temperature is already in the correct units and the gas constant is given as 8.31 JK-1mol-1. Now we are ready....
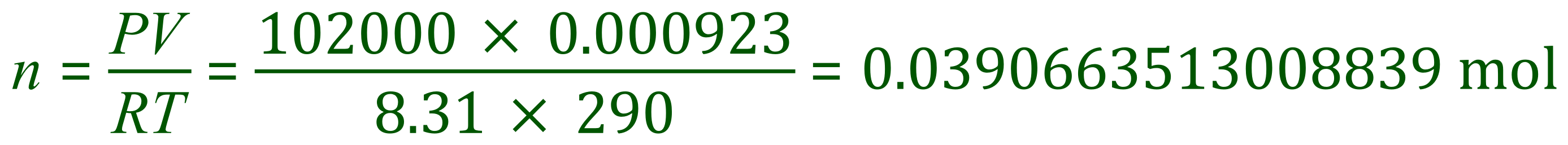
The answer is of course an insanely long decimal, but you must remember to ALWAYS work to full calculator accuracy until you are ready to present your final answer. We were told at the beginning of the question that 1.25 g of the gas was used, and we now know that 1.25 g of the gas is this many moles.
Therefore if 1.25 g of the gas is 0.0390663513008839 moles, then one mole of the gas would have a mass of:

Therefore the relative formula mass of the gas is 32.
Q. Find the mass of 200 cm³ of carbon monoxide (CO) at 17°C and a pressure of 98,900 Pascal (C = 12, O = 16).
Once again we are looking at calculating 'n'
In this question you should be able to see straight away that some of the units are not as they should be to be directly plugged into the ideal gas equation. We need to rearrange the ideal gas equation in terms of the number of moles 'n' and convert all of our given quantities to the appropriate units.
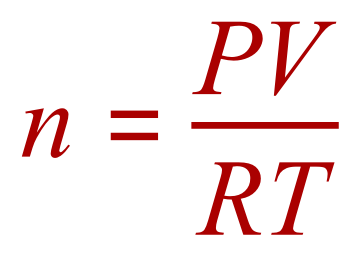
Our pressure is correctly represented in Pascal already so this doesn't need to be altered, temperature is represented in degrees Celsius so we need to convert this to Kelvin by adding 273 to the value which makes it 290 Kelvin and finally 200 cm³ needs to be converted to cubic metres, by division by 1 million. This makes our volume 0.0002 m³. We are now ready to "plug and play" as it were.
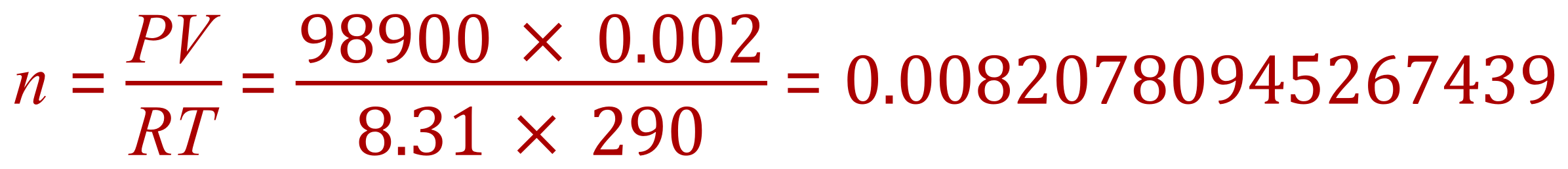
Remembering full calculator accuracy, we now have the number of moles of the gas concerned. We are given the values of the relative atomic masses of carbon as 12 and of oxygen as 16 so we can establish that one mole of carbon monoxide would have a mass of 28 g.
If one mole of carbon monoxide has a mass of 28 g, then 0.00820780945267439 moles of carbon monoxide will have a mass of:

Q. Calculate the volume occupied of 0.1g hydrogen gas (H2) at 293 K and a pressure of 100 kPa (H = 1)
This time, we are still using the ideal gas equation but we are being asked to produce a value for the volume of gas, therefore ultimately we will rearrange the formula/equation in terms of V. First of all let us examine the information we've been given.
We have a value for P in kilo pascals so we therefore need to convert this to Pascal, this would be 100,000 Pascal. We have a temperature which is already in the correct units so this doesn't need to be touched. We have been given the value of the gas constant R and we can calculate the number of moles 'n' from the mass of the gas and knowledge of the mass of one mole of hydrogen. Incidentally, we are given a value for the relative atomic mass of hydrogen as one but the question involves a diatomic hydrogen gas so we will need to adjust the value for our calculations to '2'
Let's now "plug and play" :
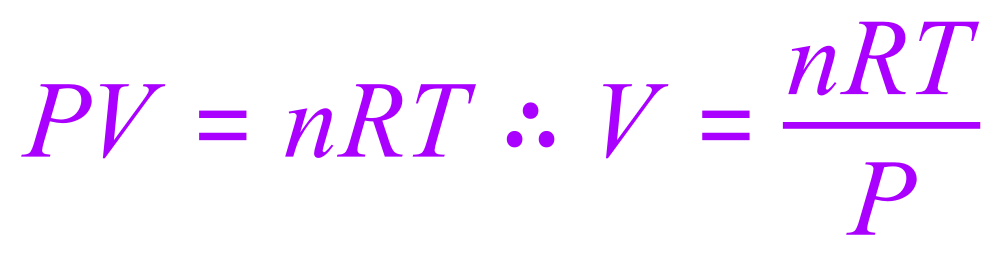
First of all let's calculate the number of moles. We are told that we have 0.1 g of hydrogen gas, and we know that the mass of one mole of diatomic hydrogen is 2 g, therefore the number of moles of hydrogen (n) would be:
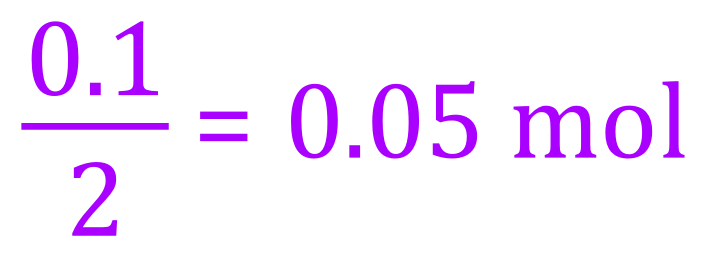
If we now substitute these values into the rearranged form of the equation, we can evaluate a value for the volume which will of course come out in cubic metres.
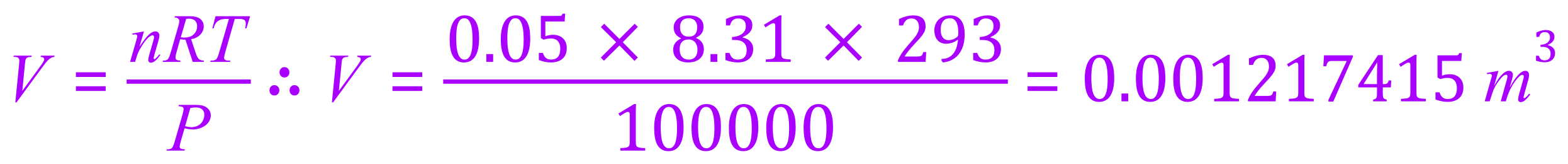
This is of course our answer, but sometimes we need to reduce it to another unit just so that we can actually visualise the amounts we are talking about. While 0.001217415 m³ is correct, to rationalise this in your mind we would probably consider converting this to cubic centimetres, a unit which will more familiar with in the laboratory environment.
In this case our value would come to 1217.4 cm³, 1.22 cm³ or just under 1 1/4 L.
Q. The hydrocarbon gas Ethane burns in oxygen according to the equation:

(a) What volume of Oxygen would be required to burn 1 dm3 of Ethane?
We are given the balanced equation for the complete combustion of Ethane in excess oxygen (we say excess to make sure that the combustion is in fact complete, but we can see from the equation just how much oxygen is actually required).
2 moles of Ethane requires 7 moles of diatomic oxygen to completely combust into 4 moles of carbon dioxide and 6 moles of water.
This question is simpler than it might first appear, because we know now that one mole of a gas at room temperature and pressure occupies 24 dm3 so we can restate the problem by saying that according to the equation 48 dm3 of Ethane would require 168 (7 x 24) dm3 of Oxygen, so it's a simple calculation to show that one cubic decimetre of Ethane gas would require:
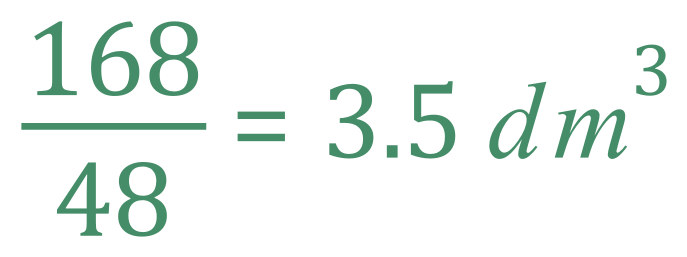
(b) What volume of Carbon Dioxide would be produced?
Let us consider the equation once more:

There are a couple of ways to attack this, but they are all quite simple as we are dealing purely with molar quantities and therefore ratio values. The equation tells us that 2 moles of Ethane requires 7 moles of Oxygen to produce 4 moles of carbon dioxide and 6 moles of water.
We calculated previously that the volume of oxygen required would be 3 1/2 cubic decimetres, so from a simple ratio point of view you should be able to see that the amount of carbon dioxide that would be produced would be 4/7 of this amount:
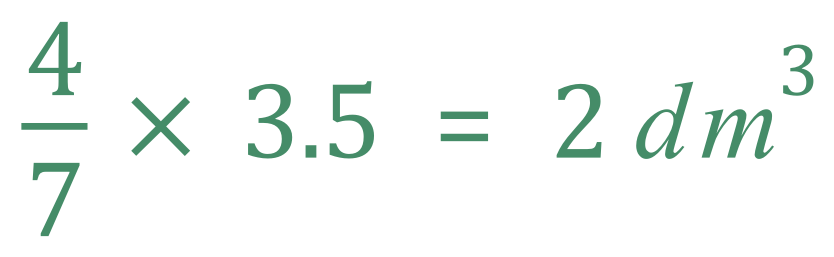
Another way of looking at it is if we consider the molar volume of the gas as 24 cubic decimetres, then we can see that we would burn 48 cubic decimetres of Ethane to produce 96 cubic decimetres of Carbon Dioxide, therefore one cubic decimetres of ethane would produce 96÷48 = 2 cubic decimetres of Carbon Dioxide.
Q. 20 cm³ of a hydrocarbon needed 90 cm³ of oxygen for complete combustion. 60 cm³ of carbon dioxide was produced. All volumes were measured at room temperature and pressure. Find the formula of the hydrocarbon.
In calculations such as these when we are asked to find the formula of the hydrocarbon it is usual to represent the unknown using variables for the numbers of carbon atoms and hydrogen atoms respectively, so for example the hydrocarbon in this case might be represented with 'x' and 'y' where the numbers of atoms would normally go. We know that the combustion of a hydrocarbon requires a certain amount of oxygen and produces carbon dioxide and water as the products, so we can write an equation for the combustion in this format:

From the equation we can see that one mole of the hydrocarbon reacts with 1 mole of Oxygen to produce one mole of Carbon Dioxide and 1 mole of water. We are told that 20 cm³ of the hydrocarbon requires 90 cm³ of oxygen and produces 60 cm³ carbon dioxide. We can take this one step further and say that the ratio of hydrocarbon to oxygen is 2 to 9, producing 6 units of carbon dioxide each time.
Therefore we could quite properly rewrite our equation this way:

The reason that I've put a question mark next to the water is that although we know it is produced, it is not referred to in the question, however we will be able to put a number in the place of the '?' quite soon.
From the equation we can see that we produce 6 moles of carbon dioxide, and so from our knowledge of balancing equations the value for 'x' in the hydrocarbon must be 3. By similar reasoning, as we have 18 oxygen atoms on the left-hand side of the equation and 12 of these already accounted for on the right-hand side of the equation we can see that the value for '?' must be 6.
If you're not sure about where these values come from, stop at this point and study a bit longer.
If you are okay with the reasoning, we can now state that the hydrocarbon formula would be C3H6 - potentially either Propene or Cyclopropane.

Q. 2.76 g of a particular carbonate X2CO3 were treated with an excess of dilute hydrochloric acid, and the carbon dioxide involved was collected and measured. 480 cm³ was produced at room temperature and pressure.

Calculate the following:
(a) the number of moles of the carbonate used in the experiment
(b) the mass of 1 mole of the carbonate
(c) the relative atomic mass of the element X
We are given the equation of the reaction between our unknown carbonate and Hydrochloric Acid, producing as we would expect a Chloride and Carbonic Acid which would break down into Carbon Dioxide and Water. The first part of the question is to calculate the number of moles of carbonate used in the experiment. Studying the equation we can see that one mole of carbonate produces (amongst other things of course) one mole of Carbon Dioxide. Now we are told how much Carbon Dioxide is actually produced (480 cm³) so we can convert this to moles by virtue of the fact that one mole of Carbon Dioxide would have a volume of 24 dm3 and a mass of 44 g.
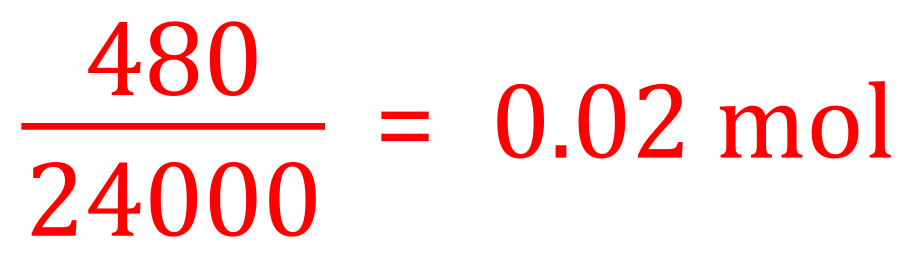
(a) Since the equation is one-to-one with respect to Carbonate and Carbon Dioxide, the number of moles of Carbonate used must also be 0.02.
(b) We are told at the beginning of the question that we have 2.76 g of the Carbonate, and we have evaluated in part (a) that this is in fact 0.02 moles. The mass of 1 mole of the Carbonate must therefore be:
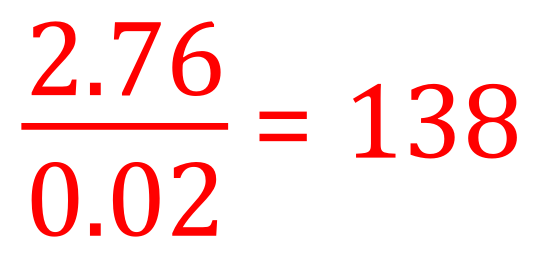
(c) As this is the mass in grams of 1 mole of the Carbonate, it must also represent the relative molecular mass. We know that the relative atomic mass of Carbon is 12 and that of Oxygen is 16, so we can produce an expression for the relative atomic mass of the unknown element X this way:
![]()
![]()
Given the fact that the relative atomic mass of the unknown element X is 39, we can conclude that it is in fact Potassium.
Q.
(a) Calculate the number of moles of gas molecules in a laboratory with a volume of 969 m³ (not including any volume taken up by benches and so forth) at a temperature of 290 K and a pressure of 99.5 kPa.
(b) Assuming that the area inside the lab contains 0.93% Argon by volume, calculate the number of moles of Argon in the lab and hence calculate the number of Argon atoms.
Take the gas constant R to be 8.31 JK-1mol-1 and the Avogadro constant to be 6.02×1023 mol-1
(a) This question, on the face of it seems quite complicated but is in fact a straightforward use of the ideal gas equation, with the usual (expected) transposition having to take place, ie: this time we need to make 'n' the subject. Let us remind ourselves of the ideal gas equation:
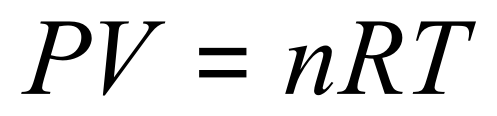
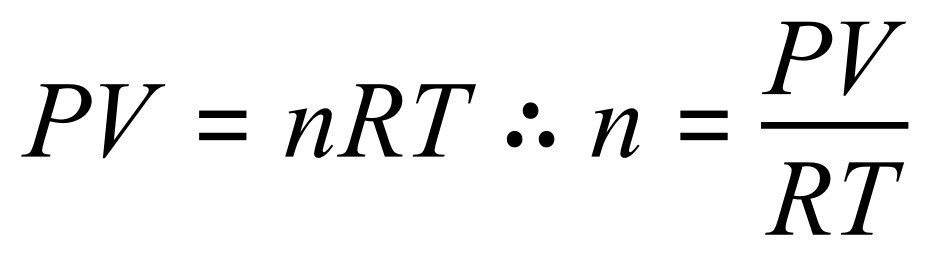
We are told that the air pressure inside the lab is 99.5 kPa which we need to convert to 99,500 Pascal, the temperature is 290 K which needs no conversion. The volume of the laboratory is also quoted in cubic metres so this value doesn't need to be changed, and finally the gas constant is given as its usual value. We can simply plug in our values to obtain an answer to part (a):
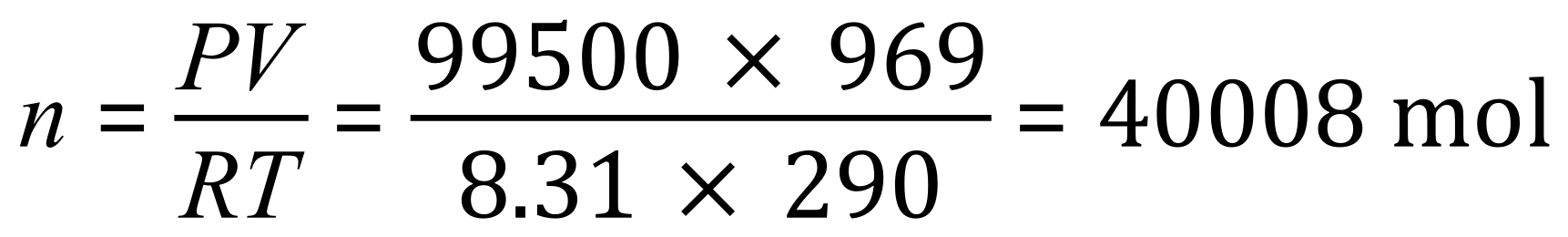
(b) We are told that the percentage of Argon in the laboratory atmosphere is 0.93%, so we can simply multiply our value for the number of moles found in part (a) above by 0.93/100:
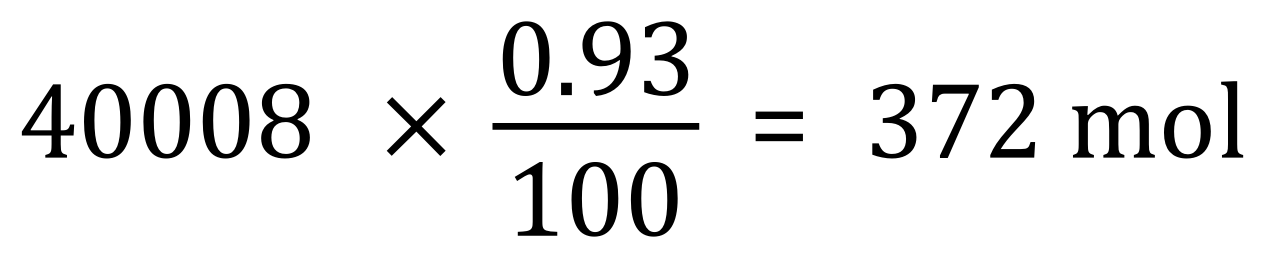
We know that one mole of any substance contains the Avogadro number of particles, therefore the number of atoms of argon in the laboratory would be the product of the number of moles and the Avogadro constant:
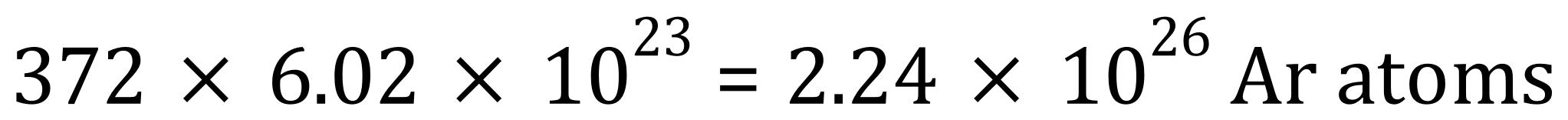
Q. Sulphur dioxide can be removed from flue gases by reacting it with calcium carbonate (limestone). If any flue gas contains 1% sulphur dioxide by volume, what mass of calcium carbonate would be needed to remove the sulphur dioxide from 1000 m³ of the flue gas.
The equation for the reaction between calcium carbonate and sulphur dioxide is as follows:

(C = 12, O = 16, Ca = 40)
The first thing that you should notice is that this is a one-to-one reaction, in other words one mole of Calcium Carbonate will remove one mole of Sulphur Dioxide producing one mole of Calcium Sulphite and one mole of Carbon Dioxide.With this information in mind we should set about working out exactly how many moles of Sulphur Dioxide we are talking about, because once we have established this, then we can see that we will need the same number of moles of Calcium Carbonate to effect this reaction.
We are told in the question that we have 1000 m³ of flue gas, of which 1% is Sulphur Dioxide. A little bit of simple mental arithmetic now tells us that 10 m³ of the flue gas is Sulphur Dioxide. 10 m³ of flue gas is 10,000 dm3. One mole of Sulphur Dioxide gas occupies 24 dm3 at room temperature and pressure (RTP).
Therefore:
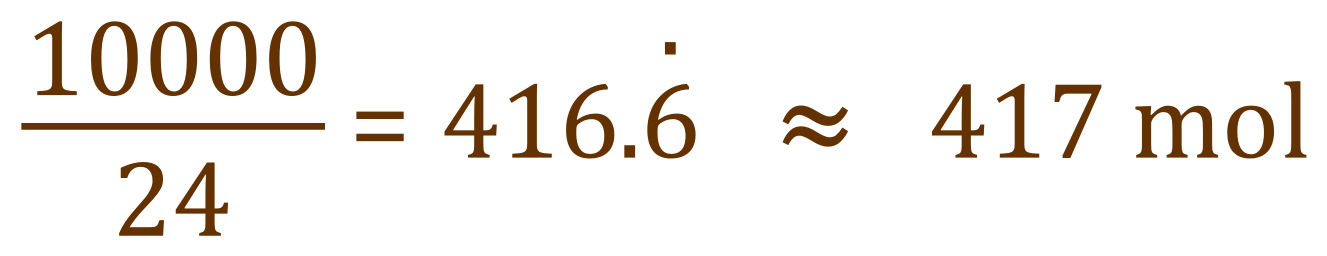
This is the number of moles of Sulphur Dioxide in every 1000 m³ of the flue gas, so we need the same number of moles of Calcium Carbonate as per the balanced equation to remove it. We are given the relative atomic masses of Calcium, Carbon and Oxygen as 40, 12 and 16 respectively so we can evaluate the relative molecular mass of calcium carbonate as 40+12+ (3x16) equals 100.
If 1 mole of Calcium Carbonate has a mass of 100 g, then the mass of Calcium Carbonate we need per 1000 m3 of flue gas is:
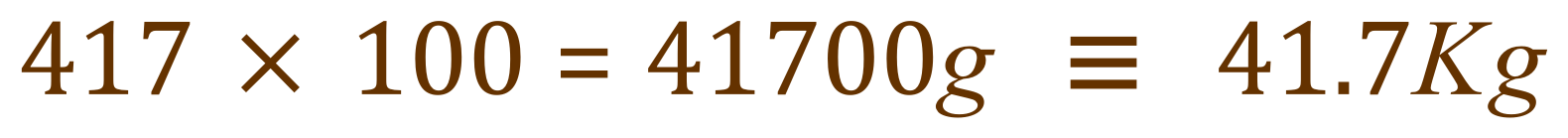
Q. 10 cm³ of an unknown hydrocarbon was sparked with 100 cm³ of Oxygen (an excess). When the resulting gases were cooled back to the original room temperature, they had a volume of 75 cm³. Exposure of these gases to Sodium Hydroxide solution reduced the volume to 35 cm³.
From this information find the formula of the hydrocarbon.
This question requires knowledge of the value for the molar volume of a gas, and knowledge of the combustion products of a hydrocarbon in oxygen. Look at what the question tells you.
What we do know is that one mole of a gas at RTP occupies 24 dm3 and that we are given 10 cm³ of it, so irrespective of the fact that we don't yet know what the gas is, we can work out how many moles of it we started with. Let us call our unknown hydrocarbon X. We can work out how many moles of X we started with this way:
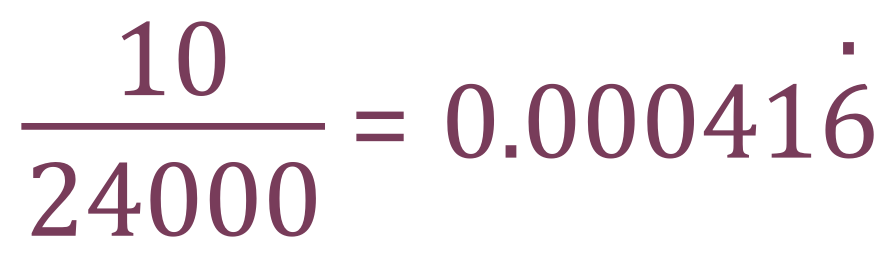
After the combustion we were left with 75 cm³ of gas, which further reduced to 35 cm³ once it was treated with Sodium Hydroxide solution. We deduce from this that 75-35 = 40cm3 of this gas was carbon dioxide, which will combine with sodium hydroxide in the following way:

Now, as we started off with 100 cm³ of oxygen which we were told was in excess we must ask ourselves "why are we told 100 cm³ if it was going to be an excess amount anyway". Remember that in an examination question, if you are given information you should expect to have to use it. We are told that we are left with 75 cm³ of gas, and that 40 cm³ of this disappears by reacting with the Sodium Hydroxide solution, therefore the remaining 35 cm³ has to be the excess oxygen (assuming that the amount of water made would be negligible by volume, as back at room temperature it would be liquid).
With this in mind, we can see that 65 cm³ of oxygen must have been used in the reaction.
Let us now take stock of what we know so far.
10 cm³ of X reacts with 65 cm³ of Oxygen to produce 40 cm³ of Carbon Dioxide. If you note that all of the volumes given so far are in cubic centimetres in this last sentence, you should be able to understand that we could regard this as mole quantities and say that 10 moles of X reacts with 65 moles of Oxygen to produce 40 moles of Carbon Dioxide. Let us simplify this a little bit by restating it as one mole of X reacts with 6.5 moles of Oxygen to produce 4 moles of Carbon Dioxide:

The above equation needs a little bit of explanation.
We agreed on 6.5 moles of oxygen molecules, but this would of course become 13 moles of oxygen atoms. We know that we produce 4 times as much carbon dioxide as we did hydrocarbon X to start with (40 cm³ CO2 from 10 cm³ of the hydrocarbon X) so we can start looking towards hydrocarbon being "C4" something, but until we've worked out the number of hydrogen is present we don't know whether we are dealing with an alkane, alkene, alkyne or cyclo compound.
We start with 13 Oxygen atoms, and if we inspect the right-hand side of the equation above we can see that 8 of these are used up in the Carbon Dioxide. Due to the Law of Conservation of Mass we cannot lose or gain Oxygen therefore must have 5 molecules of water to account for the missing 5 Oxygen atoms.
Our equation therefore becomes:

Thus identifying our hydrocarbon X as C4H10 (Butane).
Back to >> Questions <<
Back to >> Ideal Gas Law <<