[A] Titrations
Perhaps one of the most fundamental investigations ever to be completed in chemistry is the "titration" or as it used to be known "volumetric analysis". The titration is simply an experiment that lets you see what volume of one reactant will be needed to react with a fixed volume of another reactant. The method is quite simple and involves measuring out accurately a known quantity of a known strength reactant, then carefully feeding in another reactant until the reaction is complete, this will usually be indicated using (not surprisingly) a substance called an indicator. There are many types of indicator and which particular one you use depends on the nature of the titration you are conducting. To complete the relatively straightforward mathematics involved in the titration, a good knowledge of moles and molarity is required.
Q. A student measures 25 cm³ of 0.5M sodium hydroxide solution into a conical flask and adds phenolphthalein as an indicator. The student then titrates this solution with dilute hydrochloric acid of unknown concentration, and finds that the average of three titrations requires 17.5 cm³ of the unknown strength acid to reach the end point. Given this information, calculate the concentration in moles per litre of the acid used.
A. In all of this questions the first thing that we should consider is the balanced chemical equation for the reaction taking place:

This is a particularly simple neutralisation reaction, involving a one-to-one ratio of hydrochloric acid and sodium hydroxide solution. Given the generic "acid plus base equals salt plus water" we can see that one mole of hydrochloric acid will react with one mole of sodium hydroxide (both in solution of course) to produce one mole of sodium chloride solution and one mole of water. Because we have used 0.5 molar sodium hydroxide solution we can say that half a mole of sodium hydroxide solution will take half a mole of acid to neutralise it. So what we need to calculate now is how many moles we actually did use?
25 cm³ of our sodium hydroxide solution would contain:
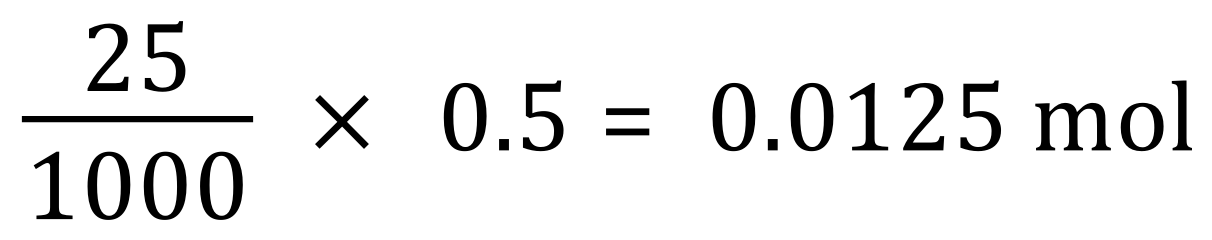
The result of this calculation 0.0125 mol tells us that this was the number of moles of sodium hydroxide in the initial 25 cm³. So, how many moles of hydrochloric acid did we actually use?. Well, go back to the balanced equation and you can see that the reaction is in fact one-to-one, so if we used 0.0125 moles of sodium hydroxide then we must also have used the same number of moles of hydrochloric acid. Study this for a while if you're having trouble understanding where my conclusions have come from. This can be quite tricky and indeed it did take me (the author) quite some time to understand this type of problem myself.
Okay, we now know that we have used 0.0125 moles of hydrochloric acid and that this was contained in 17.5 cm³ of the solution. The final step of our calculation is to work out how many moles would be contained in 1 L of the acid, which would be the molarity of the acid, and the answer to the question posed. If 17.5 cm³ contained 0.0125 then one cubic centimetre would contain 0.0125÷17.5 which works out at 0.000714285 moles. Before I continue with the calculation I need to to explain that you should always use full calculator accuracy and never be tempted to round numbers until the very end and indeed then only to the precision that you are asked for. It is highly unlikely that a solution of 0.000714285 could ever be regarded as accurate so this is enough decimal places for me to continue. We have no established how many moles of hydrochloric acid we having one cubic centimetre of our solution, so if we then multiply this by 1000 we will arrive at our final concentration.
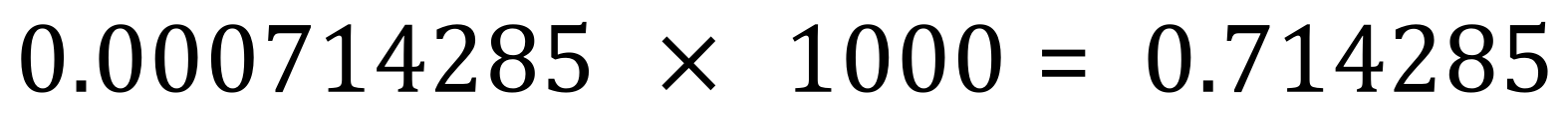
We can now of course round this to a suitable number of decimal places, and I would state that the molarity of our hydrochloric acid in this instance would be 0.71 moles per litre (or moles per decimetre cubed). This is the answer to our question.
These calculations can be quite straightforward when the reacting ratios are one-to-one as above. We will now consider a reaction where the ratio is not one-to-one:
Q. The same student repeats the titration but replaces hydrochloric acid with sulphuric acid and also replaces sodium hydroxide with potassium hydroxide. The concentration of the potassium hydroxide is 0.375 molar and in each titration, 25 cm³ of it is used. the average of three titrations performed with the unknown concentration sulphuric acid is 11.3 cm³.
A. The equation for the reaction is as shown below:

Looking at the balanced equation we can see that one mole of sulphuric acid in aqueous solution will react with two moles of potassium hydroxide in aqueous solution to produce one mole of aqueous potassium sulphate solution and two moles of water. We are told that our potassium hydroxide solution has a concentration of 0.375 moles per litre and each titration 25 cm³ of it is used. Working through the problem in a stepwise fashion as we did for the first one we first of all need to calculate how many moles of potassium hydroxide are contained in 25 cm³.
This is quite easily arrived at using the expression below:
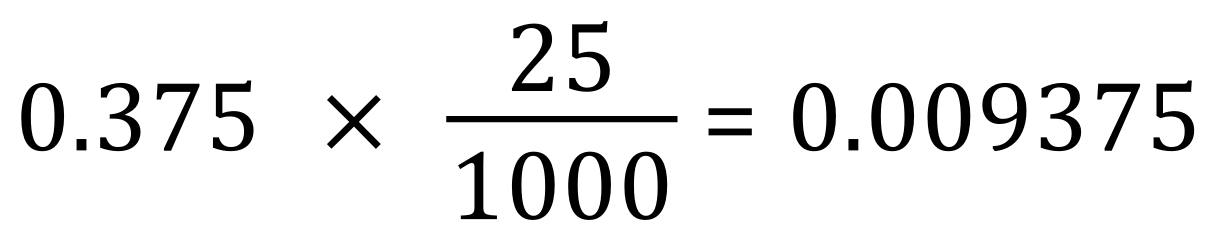
We can see now that 0.375 molar potassium hydroxide contains 0.009375 moles in 25 cm³, and that this is neutralised by HALF of this amount of sulphuric acid, can you see why?
Well, this reaction is not one-to-one as the first one was, it is a two to one reaction where two moles of potassium hydroxide are needed to react fully with one mole of sulphuric acid. Logically then we will have used 0.009375÷2 moles of sulphuric acid to complete the neutralisation. And this will be contained in 11.3 cm³ as this was the average of our three titrations.
A simple bit of mathematics will tell us that if there are 0.0046875 moles of sulphuric acid in 11.3 cm³ then the must be:
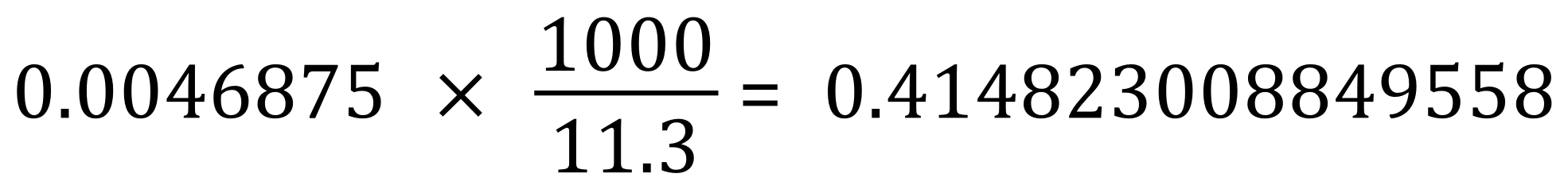
Given the fact that our potassium hydroxide solution was quoted to 3 decimal places, we would conclude that the sulphuric acid solution should similarly be quoted and therefore concentration 0.415 moles per cubic decimetre / moles per litre.
Go To >> Questions <<
Return to >> Calculations Regarding Concentrations of Solutions <<
Return to >> Acids and Alkalis <<