Factorisation
The reverse procedure to an expansion is factorisation. Just as we multiply out the factors to expand, we extract the factors and take them outside the expression to factorise. Let’s take a look at a simple example and hopefully this will become a bit clearer.
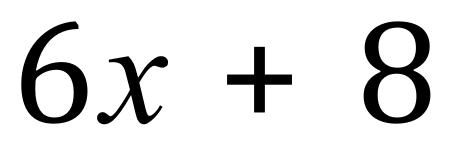
This is a simple expression with no fixed solution because ‘x’ can be anything, but what we can do is factorise it.
We need to look at both components, “+6x” and “+8” and try to see if there is any factor common to them both, in other words is any number that will go into 6 and also go into to 8?
You can probably already see that 2 will go into each one, this can’t be 2x because the eight doesn’t hold an x, the 8 is simply a constant value not a variable, so because of this we can only look for numbers. There is no number higher than 2 that will go into 6x or 8 so we “extract” this factor, leaving what is left inside brackets:
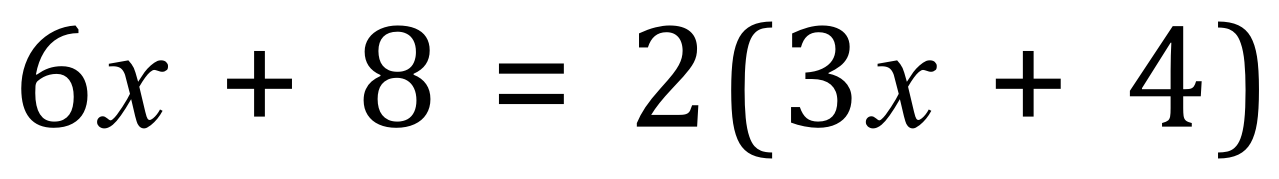
To prove that this is correct, you can if you want to expand the expression on the right, and you should end up with the expression on the left. Congratulations! you have just factorised and expanded!
Things can start to become a little bit more complicated, either when the number of components making up the expression starts to increase, or the number of variables increases, let’s take a look at an example:
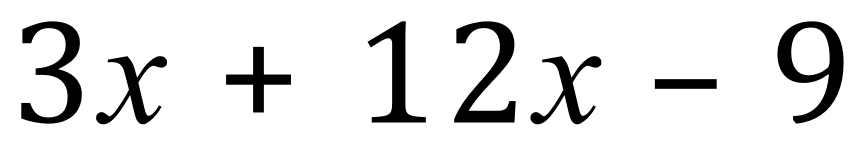
This time we have three components in the expression and we need to identify factors that will satisfy all three. In this particular case I have made it obvious that it is the number three that we need to take out of the expression and group what is left in brackets.
Q. Why does it have to be number 3, why can’t it be 3x?
A. Because the “-9” does not hold the variable “x”
The result of our newly factorised expression is this:
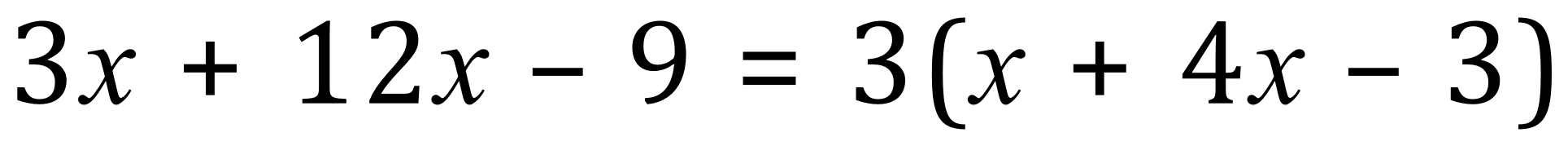
Of course, you won’t often see x’s like this being added together, the above expression would normally be written simply as 15x-9 but I broke it up deliberately just to show you how to factorise it.
>> Questions <<