The Chain Rule
Suppose that we want to differentiate this expression:
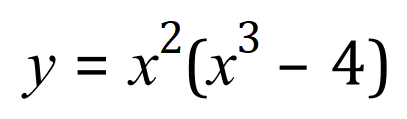
We do in fact have the product of two functions, the one outside the brackets and the one inside the brackets. This is also (potentially) a job for the product rule but let’s look at what we can do here.
In fact we can simply multiply out and then apply the Sum / Difference rule:
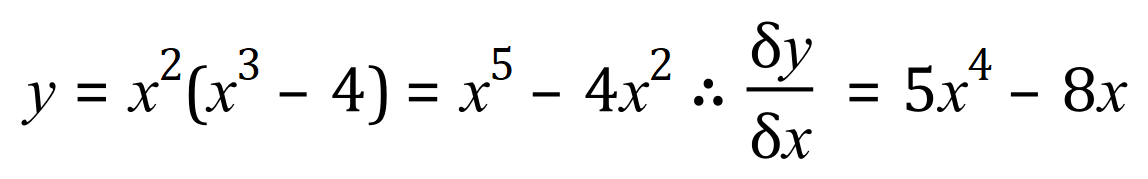
This is correct, but you might reconsider simply expanding and then differentiating if you come across an expression like this one:
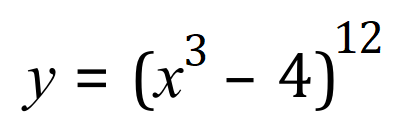
Unless you are masochistic enough to want to expand the second expression I think you would probably look for alternative way to deal with this. So, how do we get round this? Well the first thing we need to do is to convert the expression into something that is more obviously differentiable and we do this by substituting a single expression for the expression inside the parentheses:
Let us call the expression inside the parentheses ‘u’:
Therefore

Are you with me so far? If not re-read this section until you are happy to carry on. If you are with me so far then we will proceed.
To differentiate this expression we need to use “The Chain Rule” which, when you look at it is a bit like a daisy chain where one element links to the next, and to the next, and to the next and so on:
The Chain Rule states:
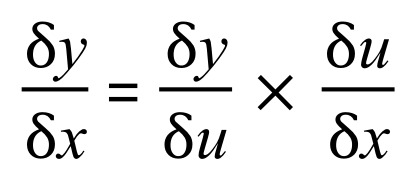
So now, let us look at our expression once again:

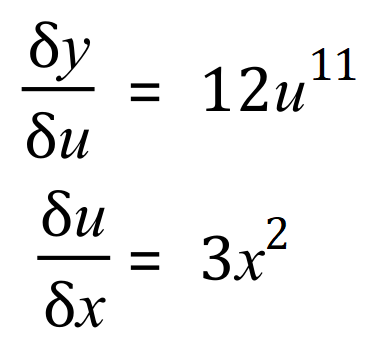
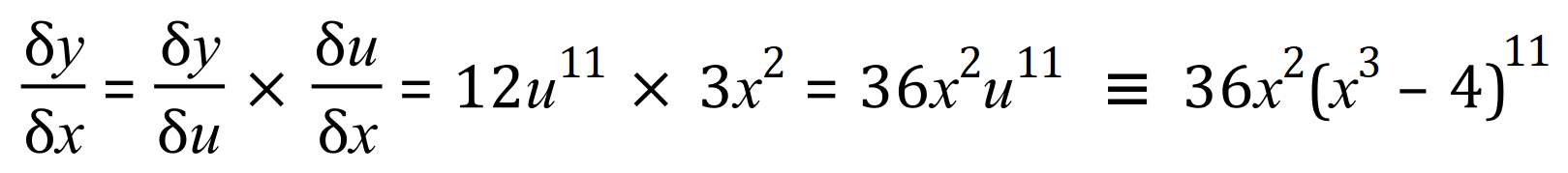
Let’s look at another example:
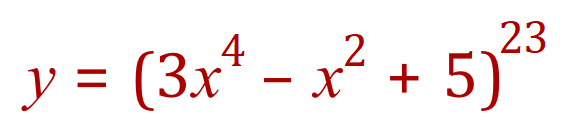
I’m sure you’ll agree that this is a bit of a beast but in reality it’s probably no harder than the previous one (but probably a little bit more tedious and will require a little bit more care) if you apply the rules and think about what you’re doing.
Let’s take it step by step:
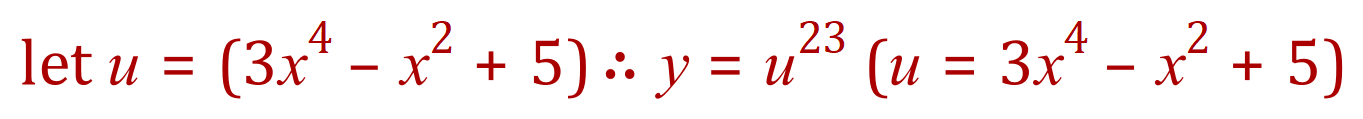
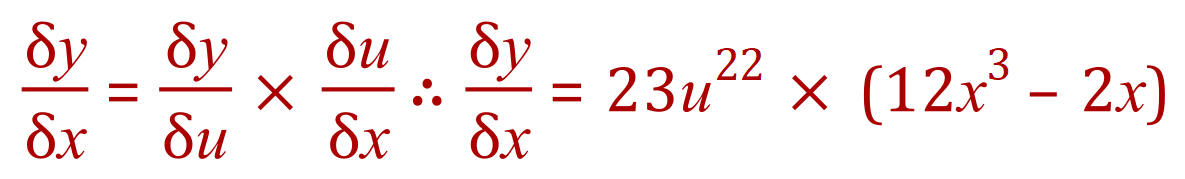
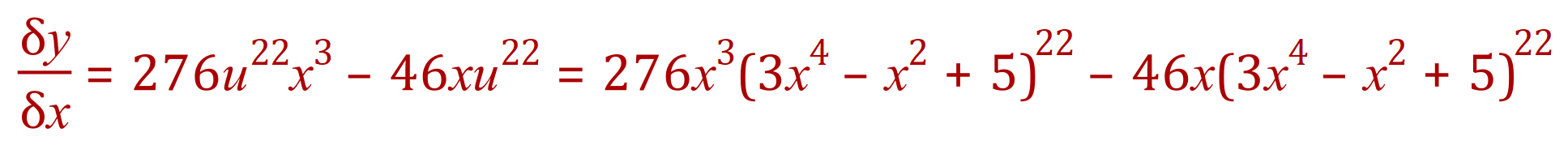
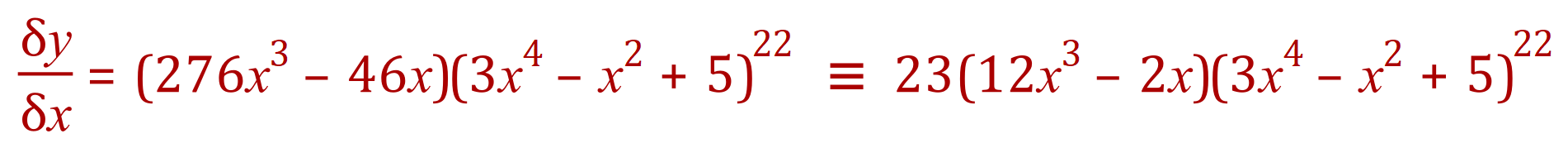
Go To >> Table Of Standard Derivatives And Integrals <<