The Product Rule
The product rule is used when two functions need to be multiplied together. In simpler cases it easier to just multiply them together and then apply the differentiation, but this isn’t always possible so we need another method to tackle this problem.
Generally in calculus, we speak of ‘functions’ such as ‘the function (u)’ and ‘the function (v)’ , this is done as a sort of “shorthand” so that the full functions don’t have to be printed repeatedly on the page, this would just lead to confusion. Another reason for doing this is that rules such as product rule, quotient rule and so on are easier to write down when using single letters, and when you start to apply these functions you simply make substitutions where necessary.
If we consider two functions ‘u’ and ‘v’ then the product rule states that the derivative of 'u' * 'v' (or 'uv') is this:

Let’s take a look at an example using simple polynomial functions (that is just x’s and powers, no trigonometric functions such as sine cosine and tangent just yet).

This is a perfect example of a polynomial function where you would / could simply just multiply out and then differentiate:
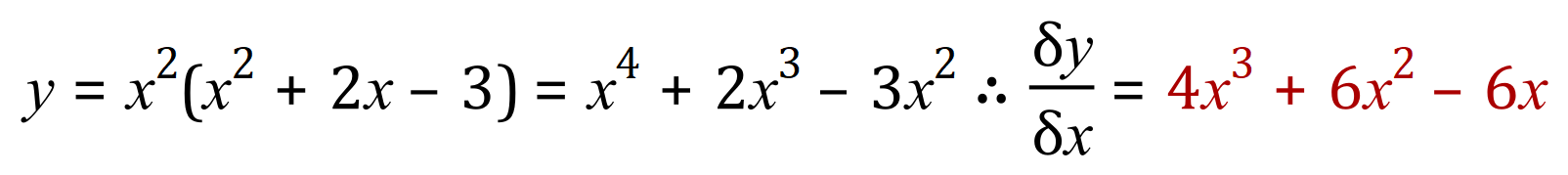
But there is no real reason why we can’t apply the product rule just to show it works:
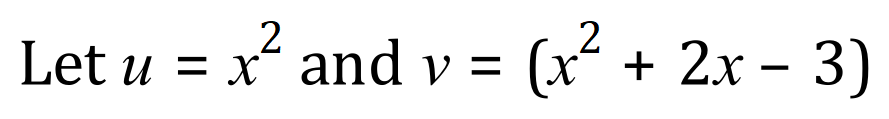
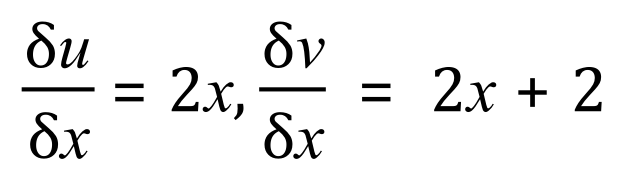
So:

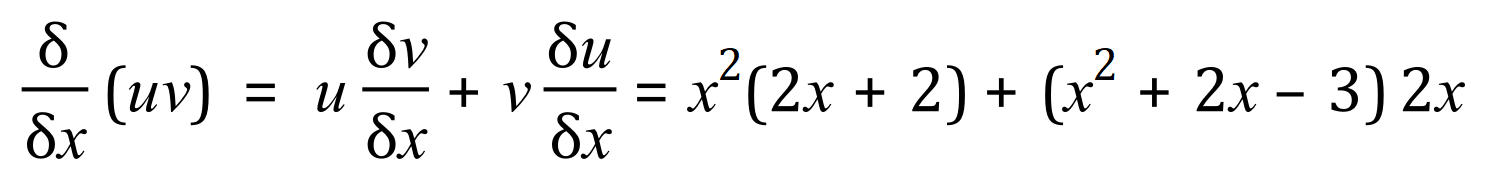
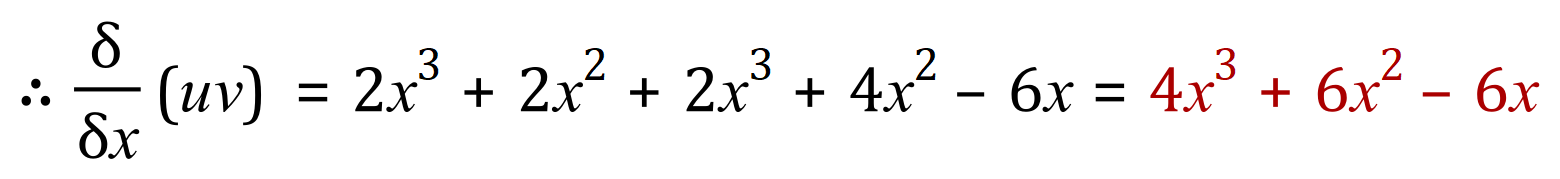
The product rule really comes into its own when you’re talking about functions involving sine cosine and tangent, and the functions ‘e’ and ‘ln’. In another document in this series I will list some “standard derivatives” and in the integration section some “standard integrals”.
Previously we showed how we arrived at the formula for simple differentiation:
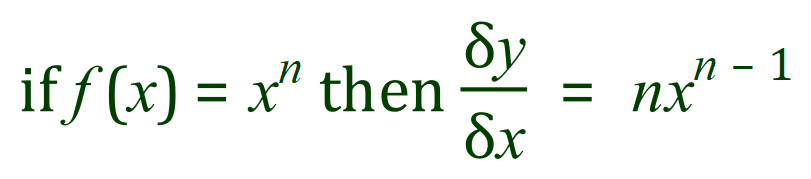
And the results of the standard derivatives and integrals can be similarly show, but the proof of these functions and how we get to them is way beyond the intention of these documents so with this in mind I ask that you just accept the list of standards without going through rigorous proof of their validity.
Because, in this part of the document I will want to use some basic trigonometric functions I will replicate a small amount of the “standards” below:

Now that we have table to refer back to, I can use the product rule with some trigonometric and polynomial examples.

Example:
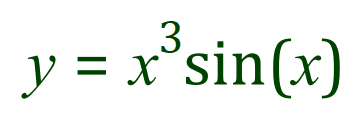
As before we allocate ‘u’ and ‘v’
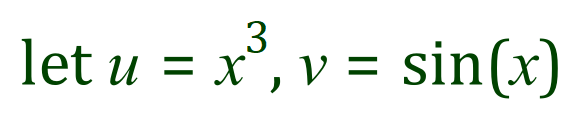
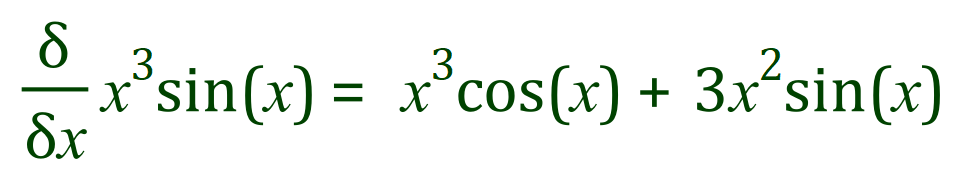
Example:
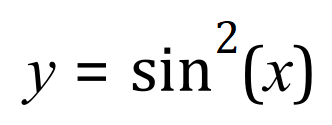
In this case, u=sin(x) and v=sin(x) because sin2(x) is (sin(x)*sin(x))
This isn’t quite as scary as you might think, for simplicity I have already include the first step I would make.This particular example has two ways of being solved, we can use the product rule in which case ‘u’ and ‘v’ will both be sin(x):
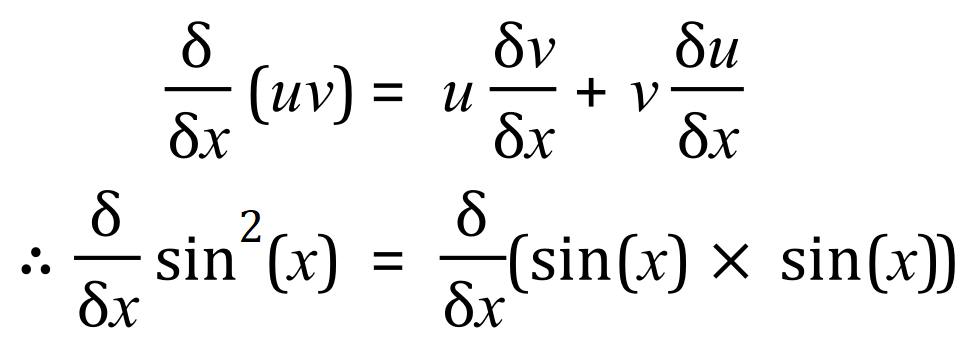
![]()
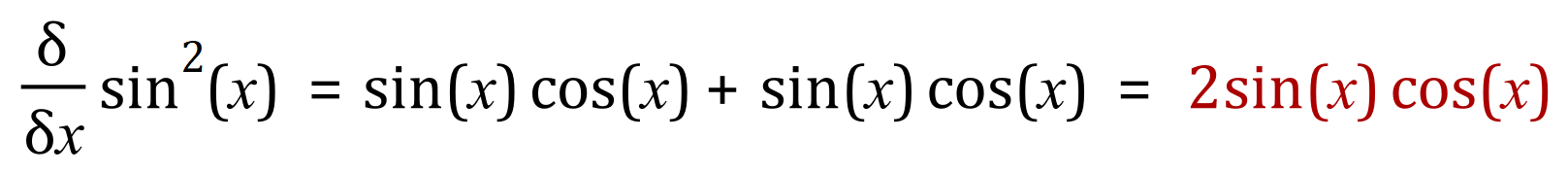
Alternatively we can use the “chain rule” (coming soon, click >> here <<):
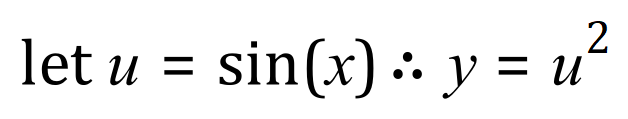
Now:

Go To >> Table Of Standard Derivatives And Integrals <<