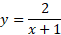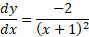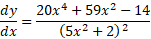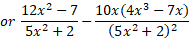The Quotient Rule
We use this rule when we wish to divide one function by another. The ‘generic’ expression for the quotient rule looks a little bit more complicated than for the product rule:
If we consider our functions ‘u’ and ‘v’ then the quotient rule states:
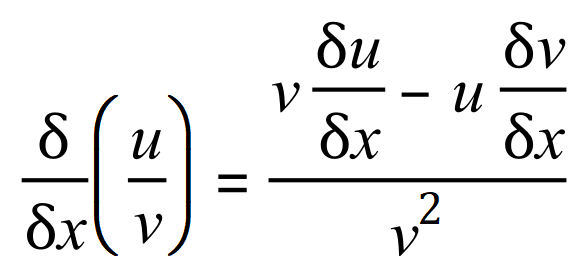
Example:
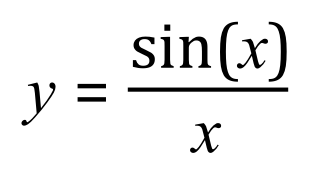
Let u = sin(x) and v=x:
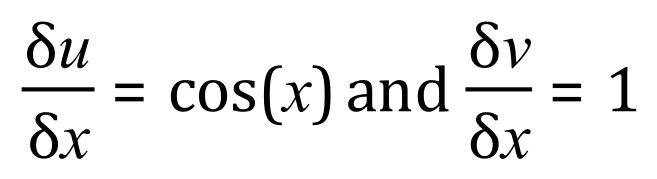
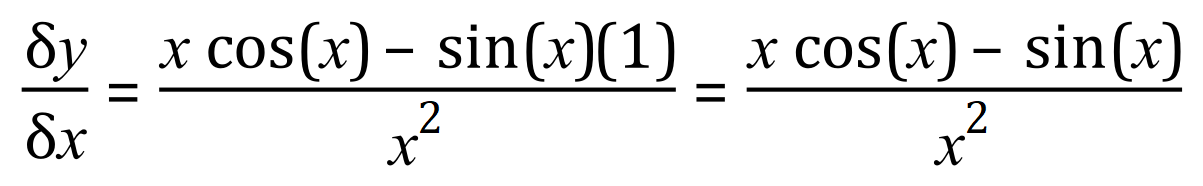
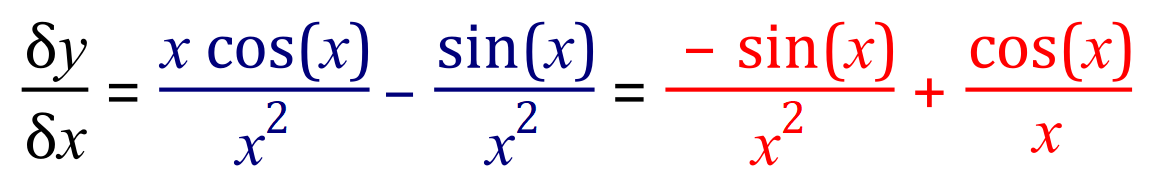
It is important to simply the answer as far as possible and although in the step I have highlighted in blue you would expect the answer to be portrayed with the cosine function first it seems to be a mathematical nuance to display the squared power in the sine function denominator first (although if you left it as I did in blue and then cancelled out the x in the cosine expression you would not, I would think at least, lose any marks for that).
Let’s take a look at another example:
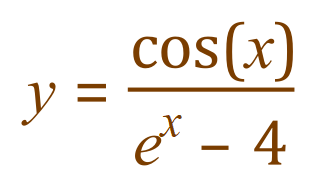
In the table of standard derivatives I gave you earlier, unfortunately I didn’t include the derivative of which is in fact
which is in fact . You will need to know this to attempt the example above. We work through the problem in exactly the same way as before:
. You will need to know this to attempt the example above. We work through the problem in exactly the same way as before:
![]()

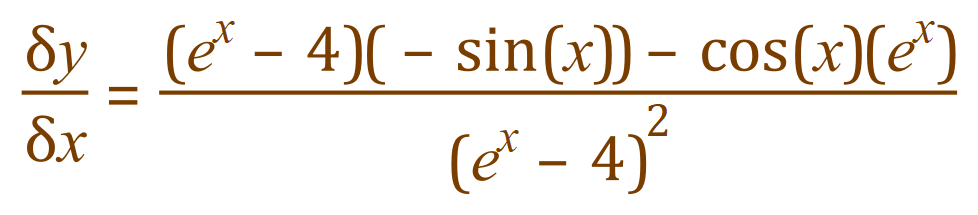
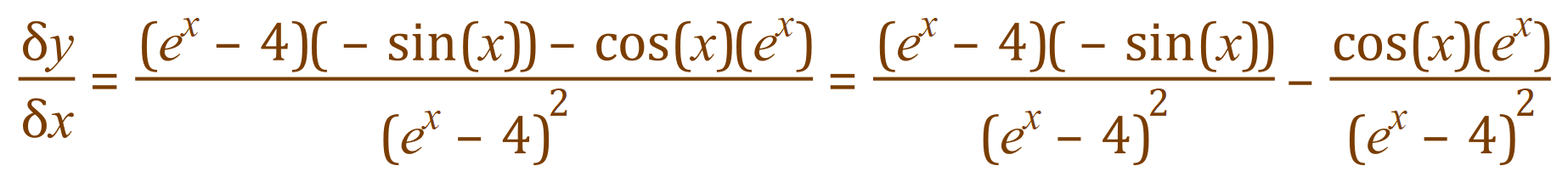
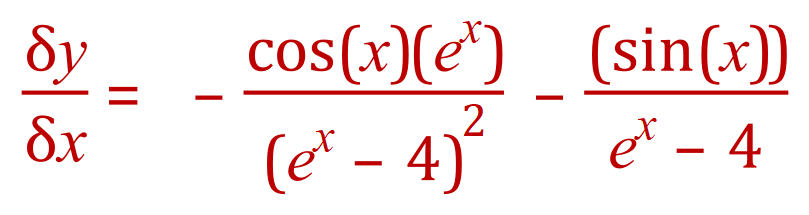
>> Questions <<
Go To >> Table Of Standard Derivatives And Integrals <<
Have a go at these examples:
|
|
|
|
|
|