The Grid Method
Mathematics has always seem to be problematic for most students. It seems to be one of those subjects that you either love or hate and very little room for "middle ground". With this in mind, mathematics teachers all over the world are constantly looking for ways to simplify those areas that seem to confuse younger students, such of those in primary on the verge of senior school. Long multiplication and long division seem to be two of the main protagonists and so the next few pages will deal with a couple of ways in which long multiplication appears to have been simplified.
First of all we'll take a look at the "grid method" for long multiplication.

There is a section on multiplication anyway in this book but consider the numbers shown above in the red box, 794 and 458. If the question was to multiply these 2 numbers together, historically students would have been taught to "drop a zero" underneath the 8 and the 5, then multiply the 4 on the bottom line by the 4 on the top line, then the 9 then the 7 ending up with 79,400. The student would then be told to "drop a zero" under the 8 in the lower line, then multiply all of the numbers in the top line by 5, that is 5×4, 5×9 and then finally 5×7. The final step would be to multiply the 8 by the 4, then by the 9 then by the 7. The student would then end up with 3 rows of numbers which would simply be added up to obtain the final answer.
Multiplication methods moved on and this was reversed, so that the multiplication by 8 was considered first, then the 5 then the 4. This would simply give the same 3 lines of numbers but in reverse order, which would then be added up before to arrive at the final answer. Both of these ways are fairly traditional but the next two ways that I'm going to discuss really do simplify matters considerably.
Hopefully you will know that "794" is made up of "7x100s", "9x10s" and "4 units". You should be able to break up the number 458 in a similar way.
The "grid method" breaks up the number, but still involves a sequence of multiplications, however these are considerably simpler and in many cases students are able to do these mentally and simply write down the answers in the appropriate boxes in the grid:
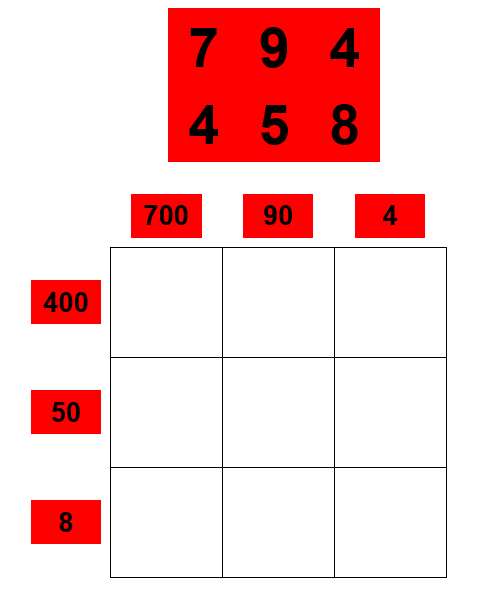
Having drawn our grid according to the number of boxes we need (multiplying together two 3 digit numbers will require 9 boxes) the hundreds tens and units are broken up as shown, and the numbers lined up as shown.
What we then do is take 2 numbers, one from the top row one from the left-hand side row, multiply the together and write the product in the box where the row and column join. So, for example 700×400 we know to be 280,000. We can do this mentally by removing zeros, multiply 7 times 4 to make 28 and then put back the 4 zeros that were taken away.
The remaining mathematical computations are completed until all 9 squares are full. The final answer is arrived at by adding up the contents of all 9 squares, and there is no necessary order to this, they can be added up in any order that you like.
