The Lattice Method
The second method that I'm going to show you is not dissimilar from the grid, but does require a little bit more care in the initial setup.
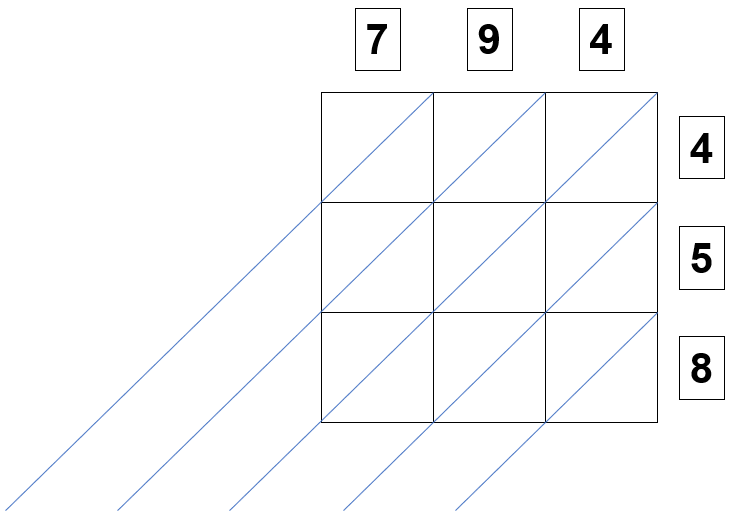
In a similar way to the "grid method", a suitable size grid is constructed according to the number of digits in the numbers to be multiplied. Just for the sake of convenience I've deliberately chosen the same numbers as before, so we need a 9 square grid (3 x 3). The obvious difference this time is that diagonal "separators" cut each square into two triangles, and these triangles are the placeholders for the products of the numbers on the intersecting lines. Let's make a start so that this is a little bit clearer.
Again there appears to be no specific order, but my advice would be to work from right to left, going down the rightmost vertical column, before moving to the one to the left and so forth.
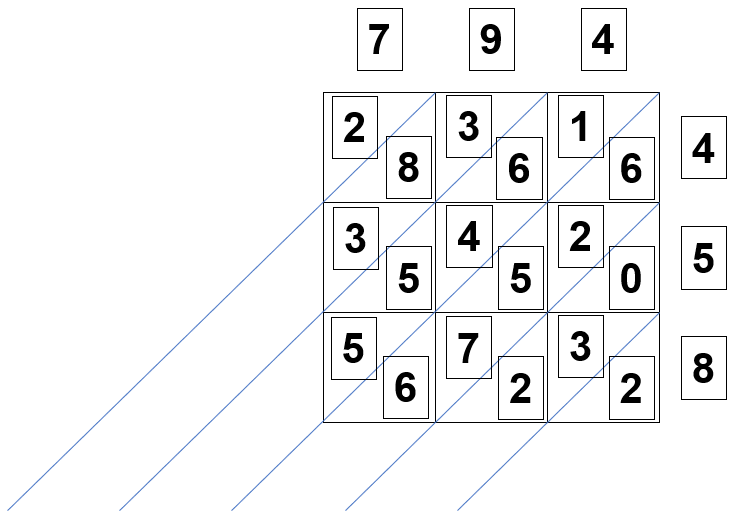
If you are pretty good with your times tables, the next part will be really simple. Let's take a look at the right hand vertical column, then the middle one and then finally the left most one:
4 × 4 = 16, 4 × 5 = 20, 4 × 8 = 32
9 x 4 = 36, 9 x 5 = 45, 9 x 8 = 72
7 x 4 = 28, 7 x 5 = 35, 7 x 8 = 56
Let's see what this looks like when these results are placed into the "lattice".
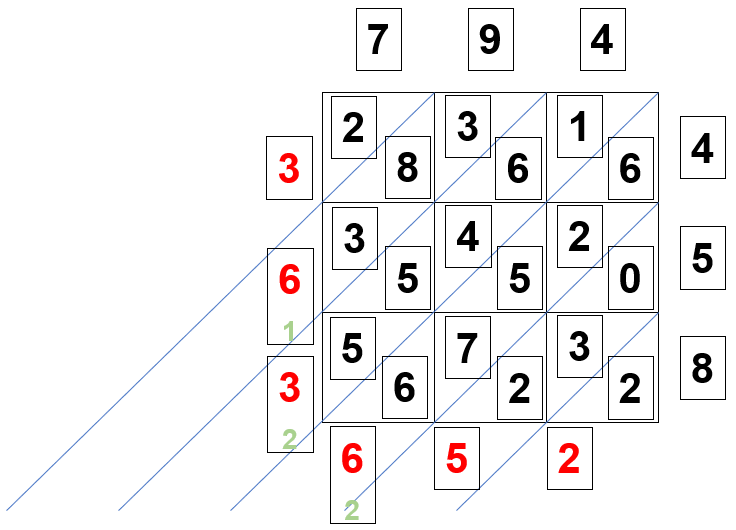
I said previously that the order in which these small multiplications were to be carried out didn't matter, but the next step (the adding up) must be done from "bottom right" to "top left" because in some cases the result of each small addition may exceed 9, in which case there will be a need to "carry".
Starting at the bottom we simply move the 2 down. We then move up left to the first "diagonal column" and we add together 0+3+2 which equals 5. We write 5 in the diagonal section outside the grid and then move onto the next "diagonal column" where we add up 6+2+5+7+6 which equals 26, we put the 6 in the diagonal section outside the grid and carry the 2.
We move up to the next "diagonal column" and add up 1+6+4+5+5 which equals 21, but of course we have 2 from the previous column which makes a total 23. We place the 3 inside the diagonal section outside the grid and once again carry the 2. We then move to the next "diagonal column and add up 3+8+3 which equals 14. We add the 2 from the previous column to make 16. We put the 6 in the diagonal section outside the grid and carry the 1. . We are now left with a single "2" in the top left "diagonal column", to which we add our "carried 1" which makes 3 in total.
If we now read the number from top left vertically downwards and then across to the right, we have our final result.....363652.